Just like resistors, we are now moving to more of a macroscopic picture of capacitors, rather than thinking microscopically about the charges on the plates. These notes will talk about combinations of capacitors in series and how this differs from resistors in series.

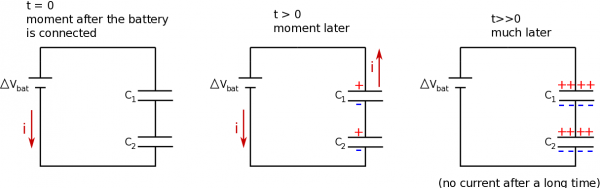
Just as with resistors, when capacitors are in series this means that all of the current that goes through one capacitor will go through the other. However, unlike resistors, the current that flows through the circuit will decrease as the capacitors charge or discharge. Since current does not actually pass through capacitors (remember that the charges get stuck on the capacitor plates), we will instead focus on what happens to the charge on the capacitors rather than the current.

Electron movement around a circuit with two capacitors - capacitors in series always have the same total charge on each plate

Consider what happens to the charge around a circuit with two capacitors in series. After the circuit is connected, electrons begin to move through the wires and collect on one plate. For every electron that gets stuck on the plate, it pushes another negative off the opposite plate. This electron continues moving down the wire (providing the electron current) until it becomes stuck on the first plate of the second capacitor. This in turn pushes an electron off the second plate of the capacitor, that continues to travel toward the battery. Because of this chain reaction, the charge on each of the capacitors in series must be the same. (This is similar to how current was the same for resistors in series.)

$$Q_1=Q_2$$