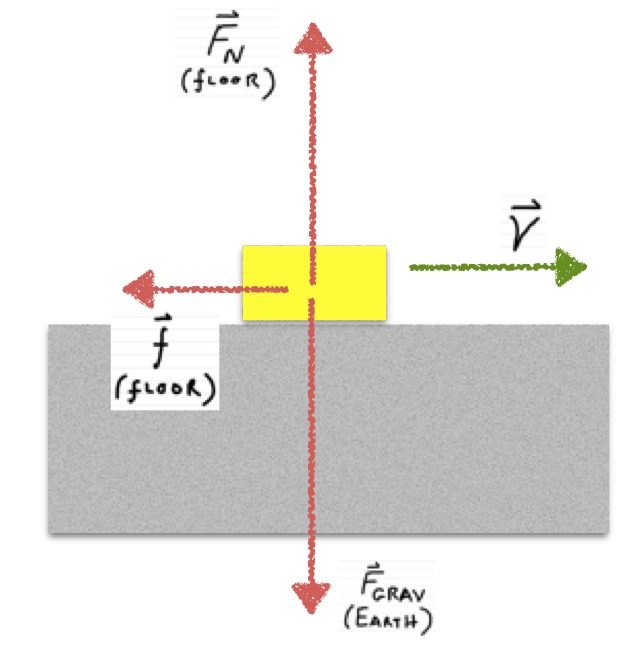
Example: Sliding to a Stop
You take a 3 kg metal block and slide it along the floor, where the coefficient of friction is only 0.4. You release the block with an initial velocity of $\langle 6, 0, 0\rangle m/s$. How long will it take for the block to come to a stop? How far does the block move?
Facts
Block is metal.
Mass of metal block = 3 kg
The coefficient of friction between floor and block = 0.4
Initial velocity of block = $\langle 6, 0, 0\rangle m/s$
Final velocity of block = $\langle 0, 0, 0\rangle m/s$
Lacking
Time it takes for the block to come to a stop.
The distance the block moves during this time.
Approximations & Assumptions
Assume surface is made of the same material and so coefficient of friction is constant.
Representations
Solution
$ x: \Delta p_x = -\mu_k F_N\Delta t $
$ y: \Delta p_y = (F_N - mg)\Delta t = 0 $
Write equation of y direction in terms of $F_N$ to sub into x direction equation.
$ (F_N - mg) \Delta t = 0 $
Multiply out
$ F_N \Delta t - mg \Delta t = 0 $
Make equal to each other
$ F_N \Delta t = mg \Delta t $
Cancel $\Delta t$
$ F_N = mg $
Combining these two equations and substituting in mg for $F_N$ and writing $ p_x = \Delta(mv_x) $, we get the following equation:
$ \Delta(mv_x) = - \mu_k mg\Delta t $
Cancel the masses
$ \Delta(v_x) = - \mu_k g\Delta t $
Rearrange to solve for $\Delta t$ and sub in 0 - $v_{xi}$ for $ \Delta(v_x)$
$ \Delta(t) = \dfrac{0 - v_{xi}}{-\mu_k g} = \dfrac{v_{xi}}{\mu_k g} $
Fill in values for variables and solve for $\Delta t$
$ \Delta(t) = \dfrac{6 m/s}{0.4 (9.8 N/kg)} = 1.53s $
Since the net force was constant we can say the average velocity can be described as: $v_{x,avg} = (v_{xi} + v_{xf})/2$, so
$ \Delta x/\Delta t = ((6 + 0)/2) m/s = 3m/s $
Sub in for $\Delta t$ and solve for $\Delta x$
$ \Delta x = (3 m/s)(1.53 s) = 4.5m $