A Tilted Segment of Charge
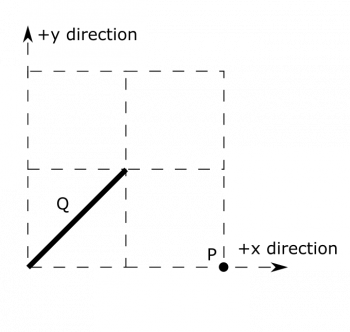
Suppose we have a segment of uniformly distributed charge stretching from the point $\langle 0,0,0 \rangle$ to $\langle 1 \text{ m}, 1 \text{ m}, 0 \rangle$, which has total charge $Q$. We also have a point $P=\langle 2 \text{ m},0,0 \rangle$. Define a convenient $\text{d}Q$ for the segment, and $\vec{r}$ between a point on the segment to the point $P$. Also, give appropriate limits on an integration over $\text{d}Q$ (you don't have to write any integrals, just give appropriate start and end points). First, do this for the given coordinate axes. Second, define a new set of coordinate axes to represent $\text{d}Q$ and $\vec{r}$ in a simpler way and redo.
Facts
- The segment stretches from $\langle 0,0,0 \rangle$ to $\langle 1 \text{ m}, 1 \text{ m}, 0 \rangle$.
- The segment has a charge $Q$, which is uniformly distributed.
- $P=\langle 2 \text{ m},0,0 \rangle$.
Goal
- Define and explain $\text{d}Q$ and $\vec{r}$ for two sets of coordinate axes.
Representations
- For the first part, we can draw a set of coordinate axes using what we already know. The first part of the example involves the following representation:
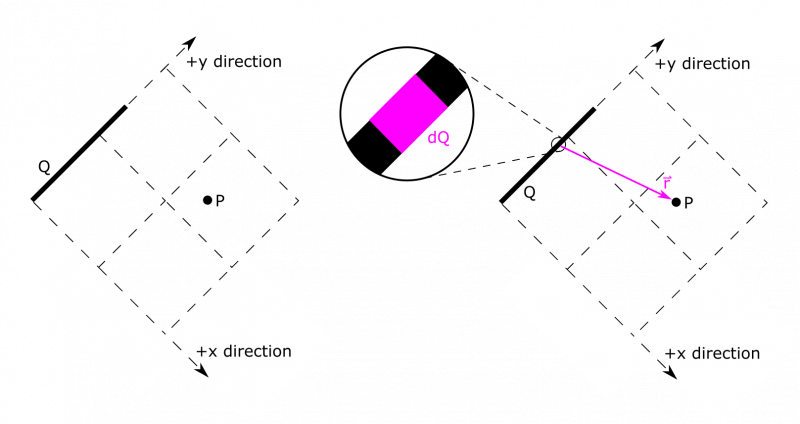
- For the second part when we define a new set of coordinate axes, it makes sense to line up the segment along an axis. We choose the $y$-axis. We could have chosen the $x$-axis, and arrived at a very similar answer. Whichever you like is fine!
Solution
Before we begin, we'll make an approximate to simplify our calculations:
Approximation
- The thickness of the segment is infinitesimally small, and we can approximate it as a line segment.
We know how to draw $\text{d}Q$ and $\vec{r}$, so we can start with an update to the representation.
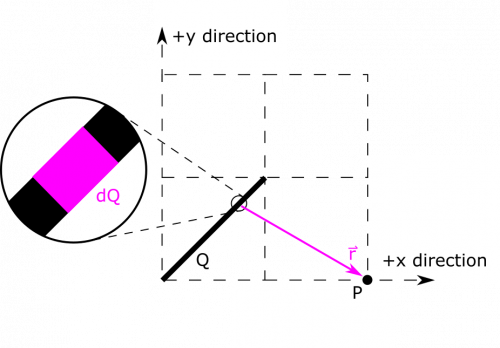
It will also be helpful to see how the dimensions of $\text{d}Q$ break down. Here is how we choose to label it:

The segment extends in the $x$ and $y$ directions. A simple calculation of the Pythagorean theorem tells us the total length of the segment is $\sqrt{2} \text{ m}$, so we can define the line charge density $\lambda=Q/\sqrt{2} \text{ m}$. When we define $\text{d}l$, we want it align with the segment, so we can have $\text{d}l=\sqrt{\text{d}x^2+\text{d}y^2}$. Since $x=y$ along the segment, we can simplify a little bit. $\text{d}l=\sqrt{\text{d}x^2+\text{d}x^2}=\sqrt{2}\text{d}x$. Note, that we chose to express in terms of $\text{d}x$, instead of $\text{d}y$. This is completely arbitrary, and the solution would be just as valid the other way. Now, we can write an expression for $\text{d}Q$: $$\text{d}Q=\lambda\text{d}l=\frac{\sqrt{2}}{\sqrt{2} \text{ m}}Q\text{d}x=\frac{Q}{1 \text{ m}}\text{d}x$$
Next, we need $\vec{r}$. We will put it in terms of $x$, not $y$, just as we did for $\text{d}Q$. A choice of $y$ instead of $x$ here would be valid had we chosen to express $\text{d}Q$ in terms of $\text{d}y$ earlier. We know $\vec{r}_P=\langle 2 \text{ m},0,0 \rangle$, and $\vec{r}_{\text{d}Q}=\langle x, y, 0 \rangle$. Again, $x=y$, so we can rewrite $\vec{r}_{\text{d}Q}=\langle x, x, 0 \rangle$. We now have enough to write $\vec{r}$: $$\vec{r}=\vec{r}_P-\vec{r}_{\text{d}Q}=\langle 2 \text{ m}-x, -x, 0 \rangle$$ Because we picked $\text{d}x$ and $x$ as our variable, we are all set up to integrate over $x$. This means that our limits of integration also have to match the total length that we want to add up in terms of the $x$ variable, which goes from $0$ to $1 \text{ m}$. So our limits of integration would be from $0$ to $1 \text{ m}$.
In the second set of axes, the segment extends only in the $y$ direction. This problem is now very similar to the examples in the notes. The length of the segment is still $\sqrt{2} \text{ m}$, so we can define the line charge density $\lambda=Q/\sqrt{2} \text{ m}$. When we define $\text{d}l$, we want it align with the segment, which is much simpler this time: $\text{d}l=\text{d}y$. Now, we can