Section 21.6 in Matter and Interactions (4th edition)
Current through a loop
Now that we have the left side of the equation, the next step is to talk about the right side of Ampere's law - namely the $\mu_0 I_{enc}$ bit. For an Amperian loop that is outside of a single wire, this part is actually rather simple, but it starts to become more complicated when we consider loops inside the wire. As we said before, if the wire is a bit thick, we can investigate what happens to the magnetic field inside the wire as well outside. That's a tough job with the Biot-Savart law and is one of the places where Ampere's law can be super useful. On this page, we will focus on the right-hand side of Ampere's law, namely, the current through our Amperian loop.
What is the current enclosed?
The point of Ampere's Law is that it relates how curly the magnetic field is to how much current produces it.
$$\oint \vec{B} \bullet d \vec{l} = \mu_0 I_{enc}$$
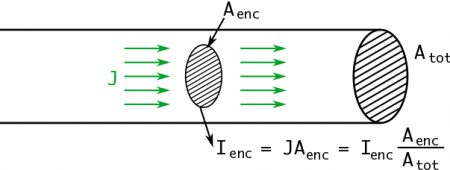
The right hand side describes the amount of current enclosed by the Amperian loop - that is, how much current runs through the inside of the loop. The figure below describes relationship between the loop and the enclosed current.
For the purposes of these notes, let's assume we have a thick wire with a total uniform current, $I_{tot}$.
Enclosing all the current
If we are looking for the magnetic field outside of the wire, we will choose to draw the loop so that it's radius is bigger than the radius of wire. In this case, the total current that runs through the wire will pass through the Amperian loop, meaning the loop will enclose all the current. This is the simplest of cases where $I_{enc} = I_{tot}$.
Enclosing some of the current
When we want to find the magnetic field inside the wire, then we need pick the radius of the loop to be smaller than the radius of the wire. In this case, some of the current will pass through the loop but not all of the current. We need to be able to determine what fraction of the total current will pass through our loop.
Just like how we used charge density when talking about the charge from a line, we will use the current density to help us find the $I_{encl}$ (or the fraction of the current that passes through the Amperian loop). If we assume a constant, uniform current, then the current density (represented by a “J”) is given by: $$J=\frac{I_{tot}}{A_{tot}}$$ where $I_{tot}$ is the total current going through the wire and $A_{tot}$ is the total cross-sectional area of the wire. The units of current density would then be $A/m^2$. Technically, current density is a vector ($\vec{J}$) that points in the direction that the charges are moving, but for our purposes, we will only be using the magnitude J.
Once we know the current density, we can use that to find the total enclosed current ($I_{enc}$). If we multiply the current density by the enclosed area (the area of the Amperian loop you chose), then that will give use the fraction of the current that passes through the loop. Mathematically, this would be:
$$I_{enc} = J A_{enc} = \dfrac{I_{tot}}{A_{tot}} A_{enc}$$
where again $A_{tot}$ is the total cross-sectional area of the wire, $A_{enc}$ is the cross-sectional area enclosed by the loop, and $I_{tot}$ is the total current in the wire. This is very similar to how you will find $Q_{encl}$ with Gauss's Law for Electric Fields next week.