Table of Contents
Math Review
The following mathematical ideas are important to understand and to be able to use as we will rely on them fairly heavily in this course. These notes will provide a review of these ideas with links to more thorough resources if you feel like you need more information about a topic.
Scientific Notation
Scientific notation is particularly useful to represent very large and very small numbers, which will show up in E&M frequently (e.g., charges are very small objects, but the forces they experience are very strong!). The basic form of a number in scientific notation is: $number \cdot 10^{exponent}$. For example, if you have a length of $x=5,430,000 m$ then in scientific notation, $x=5.43 \cdot 10^{6} m$.
Scientific notation also ties into unit prefixes, which are commonly used in physics. For example, we could write the length of $y=.00000458m$ as $y=4.58 \cdot 10^{-6}m$ or as $y=4.58 \mu m$ (micro-meters). The common prefix names, symbols and scientific notation are shown below.
| Symbol | Prefix | Factor | Scientific Notation |
|---|---|---|---|
| G | giga- | 1,000,000,000 | $10^9$ |
| M | mega- | 1,000,000 | $10^6$ |
| k | kilo- | 1,000 | $10^3$ |
| (none) | (none) | 1 | $10^0$ |
| c | centi- | .01 | $10^{-2}$ |
| m | milli- | .001 | $10^{-3}$ |
| $\mu$ | micro- | .000001 | $10^{-6}$ |
| n | nano- | .000000001 | $10^{-9}$ |
| p | pico- | .000000000001 | $10^{-12}$ |
Vectors and Scalars
Two types of quantities that are particularly important for describing physical systems are scalars and vectors.
- Scalars are quantities that can be represented by a single number (or magnitude). Typical examples of scalars include mass, time, speed, energy and volume. These quantities inherently have no direction. For example, you would never say “I have a volume of 2 m3 to the left”. In E&M, you will encounter new scalar quantities like electric potential.
- Vectors are quantities that do have a magnitude and a direction. Typical examples of vectors include displacement, velocity, force, and momentum. These quantities must have both the number and direction. For example, you could describe a car's velocity as 20 m/s (45 mph) going east or 20 m/s in the +x direction. In E&M, you will encounter new vectors like electric field.
Scalar quantities are easy to add, multiply, or divide as they are just numbers. Vector quantities require specific ways to add and multiply because they have a direction associated with them. The rest of these notes will provide a brief overview of vector math, but a more thorough review can be found here.
Vector Notation
Vectors are typically drawn as arrows. The length of the arrow represents the magnitude of the vector, and the arrow points in the same direction as the vector. The triangle end of the arrow is typically referred to as the “head” or “tip”, with the other end of the arrow being the “tail”. When drawn this way, a vector can easily be moved around in space as it is the difference between the tip and the tail that defines the vector itself. The tail of the arrow has no meaning besides what we assign it, for example, the location at which the vector quantities is measured.
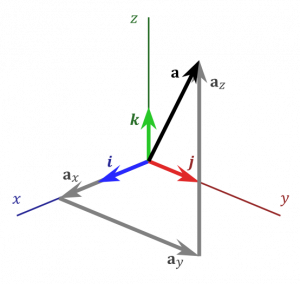
We can also define a vector in “bracket” notation: $$ \mathbf{a} = \vec{a} = \langle a_x, a_y, a_z \rangle $$ where $a_x$, $a_y$, and $a_z$ are the vector components in the $x$, $y$, and $z$ direction respectively. They tell you “how much” of the vector $\vec{a}$ is aligned with each coordinate direction. The vector itself is denoted either in bold face (typical in textbooks) or with an arrow above it.
The magnitude (or length of a vector) is a scalar quantity and is denoted by vertical lines on either side of the vector. It can be found by using the Pythagorean theorem in three dimensions: $$a = | \vec{a} | = \sqrt{a_x^2+a_y^2+a_z^2}$$
Unit Vectors
Any vector can be multiplied or divided by a scalar quantity. When you divide a vector by its own magnitude, the result is called the “unit vector.” Rather than arrow over a letter, we denote a unit vector with a “hat” over the letter.
$$ \hat{a} = \dfrac{\vec{a}}{|\vec{a}|} = \dfrac{\langle a_x, a_y, a_z \rangle}{\sqrt{a_x^2+a_y^2+a_z^2}}$$
The unit vector points in the same direction as the original vector, but it has a length of 1 and no units. This means that you can multiply a scalar value by a unit vector to give it a particular direction with out changing the value or units of the scalar. Using the idea of a unit vector, you can write any general vector in terms of its magnitude and direction: $$\vec{a} = |\vec{a}|\hat{a}$$
We also use unit vectors to describe the x, y, and z coordinate directions. These are represented by an $\hat{x}$, $\hat{y}$, and $\hat{z}$ or by an $\hat{i}$, $\hat{j}$, and $\hat{k}$. Using these coordinate unit vectors, you can write any vector in terms of its components. These are common alternative ways to write vectors (as opposed to the bracket notation). $$\vec{a} = a_x\hat{x}+a_y\hat{y}+a_z\hat{z}$$ $$\vec{a} = a_x\hat{i}+a_y\hat{j}+a_z\hat{k}$$
Vector Addition
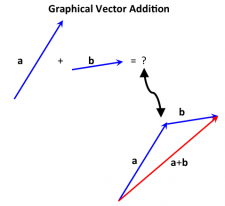
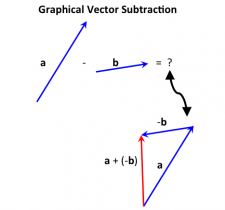
Two vectors are added (or subtracted) component by component: $$ \vec{a} +\vec{b} = \langle a_x, a_y, a_z \rangle + \langle b_x, b_y, b_z \rangle = \langle a_x+b_x, a_y+b_y, a_z+b_z \rangle $$ $$ \vec{a} - \vec{b} = \langle a_x, a_y, a_z \rangle - \langle b_x, b_y, b_z \rangle = \langle a_x-b_x, a_y-b_y, a_z-b_z \rangle $$ Note: You CANNOT simply add or subtract the magnitudes. This disregards the direction that the vectors point in. Alternatively, you can use the "tip-to-tail" method to add or subtract vectors if you have them drawn out graphically.
Vector Multiplication
Dot Product
The dot product is one way to “multiply” two vectors together, which has some important features:
- It takes two vectors and creates a scalar quantity (another name for the dot product is the scalar product).
- It measures “parallel-ness”. This is actually incredibly useful in physics. The Dot Product lets us pick out how much of one vector points in the same direction as another (i.e., how much force points in the same direction as the displacement?).
- If you dot two vectors that are perfectly parallel, you will simply be multiplying the magnitudes of each vector together.
- If you dot two vectors that are perfectly perpendicular, you will get zero.
- If you dot two vectors that point directly opposite each other, you will get the negative of the magnitudes multiplied together.
- The order of the dot product does not matter. This means that $\vec{a} \bullet \vec{b}$ will give you the same answer as $\vec{b} \bullet \vec{a}$, that is,
$$\vec{a}\bullet\vec{b} = \vec{b}\bullet\vec{a}$$
There are a couple of ways to calculate the dot product:
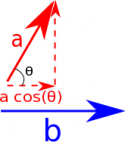
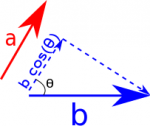
- Using vector components - If you have two vectors given by $\vec{a}=\langle a_x, a_y, a_z \rangle$ and $\vec{b}=\langle b_x, b_y, b_z\rangle$, then you can calculate the dot product by multiplying each component together and adding them together: $$\vec{a} \bullet \vec{b} = a_x b_x+a_y b_y+a_z b_z$$ - Using whole vectors and angles - You can also calculate the dot product by using the magnitudes of the two vectors and the angle between them. Using this method, it is much easier to visualize taking the parallel part of one vector and multiplying by the other vector. It doesn't matter whether you take the part of $\vec{a}$ that is parallel to $\vec{b}$ or the part of $\vec{b}$ that is parallel to $\vec{a}$, you will get the same answer. $$\vec{a} \bullet \vec{b} = |\vec{a}| |\vec{b}| cos(\theta) = |\vec{a}|cos(\theta)|\vec{b}|$$
Cross Product
The cross product is another way to “multiply” two vectors together, which again has some important features:
- It takes two vectors and creates a vector quantity (another name for the cross product is the vector product). This vector is perpendicular to the two vectors that you are crossing.
- It measures “perpendicular-ness”. This lets us pick out how much of one vector points perpendicularly to another vector (i.e., how much force helps twist a wrench?).
- If you cross two vectors that are perfectly parallel or anti-parallel, you will get zero.
- If you cross two vectors that are perfectly perpendicular, you will get the magnitudes of the vectors multiplied together.
- The order of the cross product does matter. If you flip the order of the vectors in the cross product you will get the negative answer. This means that you have pay careful attention the directions and order of your cross product.
$$ \vec{a} \times \vec{b} = - \vec{b} \times \vec{a}$$
There are a couple of ways to calculate the cross product:
- Using vector components - If you have two vectors given by $\vec{a}=\langle a_x, a_y, a_z \rangle$ and $\vec{b}=\langle b_x, b_y, b_z \rangle$, then you can calculate the cross product by using the following formula: $$\vec{a} \times \vec{b} = \hat{x}\left(a_yb_z - b_ya_z\right)- \hat{y} \left(a_x b_z - b_xa_z\right) + \hat{z} \left(a_xb_y - b_xa_y\right)$$ This formula comes from taking the determinant of a special matrix (if you have taken Calculus 3 or linear algebra already, you may have seen this special matrix before). Note that the answer to $\vec{a} \times \vec{b}$ has components in the $\hat{x}$ direction, the $\hat{y}$ direction and the $\hat{z}$ direction; however, if any of the vector components of $\vec{a}$ or $\vec{b}$ are zero, many of these terms will drop out. An example of this from mechanics is a torque in the xy-plane.
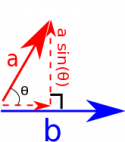
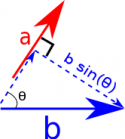
- Using whole vectors and angles - You can also calculate the magnitude of the cross product by using the magnitudes of the two vectors and the angle between them (but this does not tell you about the direction). Using this method, it is much easier to visualize taking the perpendicular part of one vector and multiplying by the other vector. $$|\vec{a} \times \vec{b} |= |\vec{a}| |\vec{b}| sin(\theta)$$ To determine the direction of $\vec{a} \times \vec{b}$ using this method, you have to use the Right Hand Rule, which was needed to understand angular momentum in mechanics. We will talk about the Right Hand Rule in detail in the second half of this course.