Table of Contents
Project 3
Project 3A: StickyStuff and the Dust Particle
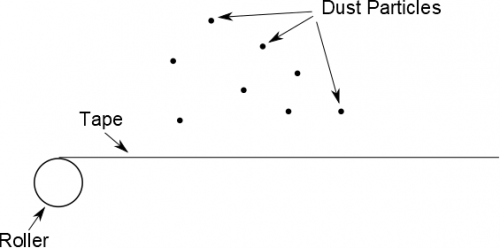
Adhesive tape is manufactured by repeatedly rolling and unrolling large sheets of plastic, which can cause there to be a charge on the surface of the tape. Why this important you may ask? Trapped in the town of Lakeview, S.P.A.R.T.A.N force has been called to the premises of StickyStuff Corporation. StickyStuff Corp has been tasked with producing a special type of adhesive tape to be used on a new top-secret spacecraft called Artemis 13. Unfortunately, there has recently been a dust problem in the manufacturing plant. Dust particles (on average, $charge=0.802*10^{-14} C$, $m=5.5*10^{-8} g$) have been accumulating on the tape as it rolls through the assembly line. The problem has been isolated to a single roller, which operates for 10 seconds at a time at a power of 100 watts (where 1 watt = 1 J/s). Using your handy-dandy-super-extender tape measure, you find that exactly 30 m of tape passes over the roller during each 10 second time period. Your team needs to determine where to put a fan and how much force the fan needs to exert on each dust particle, such that the fan blows away any dust that may be attracted to the tape. The tape must be in excellent condition before being used on the spacecraft. From your adhesive engineering education, you have access to a table that you think may help.
(There's actually a pretty cool “How it's Made” video here if you have time at the end.)
Learning Goals
- Create an analytic model for a line of charge
- Be able to explain how you set up each part of the integral, $dQ$, $r$, limits, etc.
- Explain how you used superposition in your solution
- Understand how surfaces become charged (particularly as an insulator in this case)
Project 3B: Better Thundercloud Model
 The storms over Lakeview have gotten worse, with an almost permanent pitch black cloud system hovering overhead. A new model for the thundercloud needs to be produced to obtain a better understansding of how it is functioning. While they greatly appreciated the model you created last week for the Mapping N$\vec{E}$twork Sensory Array (MNSA), the data they are collecting from the sensors are simply not matching the model's predictions. They have concluded that modeling storm clouds as point charges was, in fact, problematic. Based on some research from the National Weather Service, it looks like a better model for clouds would be two flat sheets of charge since the negative charges in the cloud collect on the bottom of the cloud and the positive charges collect near the top.
The storms over Lakeview have gotten worse, with an almost permanent pitch black cloud system hovering overhead. A new model for the thundercloud needs to be produced to obtain a better understansding of how it is functioning. While they greatly appreciated the model you created last week for the Mapping N$\vec{E}$twork Sensory Array (MNSA), the data they are collecting from the sensors are simply not matching the model's predictions. They have concluded that modeling storm clouds as point charges was, in fact, problematic. Based on some research from the National Weather Service, it looks like a better model for clouds would be two flat sheets of charge since the negative charges in the cloud collect on the bottom of the cloud and the positive charges collect near the top.
Given that the negative charge is much closer to the ground (and headquarters), the Lakeviewians want to prioritize what the Mapping N$\vec{E}$twork Sensory Array (MNSA) around HQ will show based on the bottom of the cloud. (If you have time though, they'd be interested in whether the top of the cloud has any effect.) They have shared their model of the bottom of the most recent storm cloud (which is thankfully fully functioning, well-commented code), but they are having trouble getting the electric field on the ground. The Lakeviewians have asked your team for your help completing the code.
#Set up of the objects
ground = box(pos = vec(0,0,0), width=5000, length=5000, height=0.1, color=color.green)
mountains = [cone(pos=vec(-1800,0,0), axis=vec(0,1000,0), radius=700, color=vec(1,0.7,0.2)),
cone(pos=vec(-1800,0,-1600), axis=vec(0,1000,0), radius=700, color=vec(1,0.7,0.2)),
cone(pos=vec(-1800,0,1600), axis=vec(0,1000,0), radius=700, color=vec(1,0.7,0.2))]
HQ = box(pos = vec(-100,100,0), width = 15, length = 15, height= 200, color = color.blue)
cloud = box(pos = vector(0,1000,0), size = vector(500, 1, 500), color = color.white)
#Lines 13-48 create a grid of spheres to represent the bottom of the cloud (this part of the code doesn't need be modified):
#Define how many chunks to split the cloud in the x direction (define x size of the cloud grid)
nx = 10
#Define how many chunks to split the cloud in the z direction (define z size of the cloud grid)
nz = 10
#Define where the cloud should start/stop in the x direction
startx = -250
endx = 250
#Define the spacing between each chunk in the x, based on where the cloud start/stops and how many chunks there are
stepx = (endx - startx)/nx
#Define where the cloud should start/stop in the z direction
startz = -250
endz = 250
#Define the spacing between each chunk in the z, based on where the cloud start/stops and how many chunks there are
stepz = (endz - startz)/nz
#Create an empty list to store each cloud chunk
listOfCloudChunks = []
#For each cloud chunk in the x-direction
for i in range(0,nx):
#Define the x-location of the cloud chunk
xloc = startx + i*stepx
#For each cloud chunk in the z-direction
for j in range(0,nz):
#Define the z-location of the cloud chunk
zloc = startz + j*stepz
#Make a sphere at that x-z location
cloudChunk = sphere(pos = vector(xloc,1000,zloc), radius = 50, color = color.red)
#Add the sphere to the list of cloud chunks (so we can use it later)
listOfCloudChunks.append(cloudChunk)
#This part needs to be fixed and commented...
obsLocation = vector(0,0,0)
Enet = vector(0,0,0)
Q = -15
dQ = Q/(nx*nz)
k = 9e9
for chunk in listOfCloudChunks:
Enet = vector(0,0,0)
Learning Goals
- Visualize the electric field from a 2D plane of charge
- Use multiple loops to create many observation points from many charges
- Identify patterns in the electric fields between 1D, 2D, and 3D charge distributions
- Compare/contrast process for a 2D charge distribution with a 1D charge distribution