Fall 2016 Project 11

A few weeks have passed since your brush with zombie death and your group of post apocalyptic survivors have combined with a group of scientists stationed at the Thunderdome. Your multitalented group has a plan to return Earth to its former glory and it involves obtaining an AI device called HAL. HAL, if you remember, was a part of the satellite ($m_{\rm t}=4500\,{\rm kg}$) that the Carver Media Group Network (CMGN) launched, which brought about judgement day. The satellite (and HAL) was designed to communicate with Earth out to a distance of 3.8 million kilometers. As part of the electronics HAL contains a green and a red light-emitting diode (LED) mounted on the outer surface of the satellite. One of the probes ($m_{\rm p}=400\,{\rm kg}$) remains attached to a single, very stiff spring ($k_{\rm p}=5.3\times10^{9}{\rm N/m}$) that can be compressed remotely and then released to fire off the probe. You have hacked into this remote firing mechanism.

Unfortunately, a transcription error was made by Mr. Stamper, Carver's chief “engineer” when the satellite was initially launched. As a result, the satellite escaped Earth's gravity and is currently traveling in a straight line away from the Earth at a distance of 1.9 million kilometers. Its speed is nearly constant at $340\,{\rm m/s}$. The gyroscope system that keeps the orientation of the satellite constant is still working. However, an asteroid ($m_{\rm a}=9300\,{\rm kg}$) traveling at a speed of $950\,{\rm m/s}$ is on a direct collision course (in line with the Earth and HAL) and the collision is imminent. The asteroid is presently 500 kilometers from the satellite.

Your team can recapture the satellite if it can be returned to Earth. You should design a way to return the satellite to Earth. You will also need to ensure the asteroid will not collide with the satellite - damaging the probe is ok. Your team also needs to determine the minimum amount of time until the possible collision to determine if a communication from Earth can be completed in time. Your team must succeed in order to bring an end to your zombie/boar tiger/zombie boar tiger nightmare.

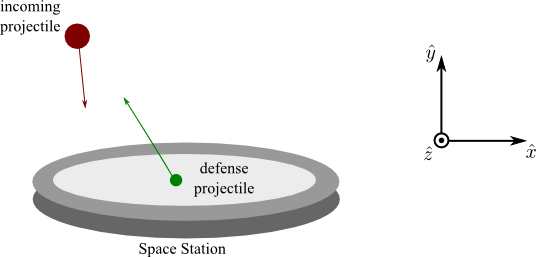
The satellite with HAL is on it's way back to Earth but behind the satellite is a number of small asteroids. A member of the recovery team, David Lightman, tells you that there is a defunct Earth defense floating space station that is very far from Earth which can be hacked into. You have been tasked with operating this projectile defense system (PDS for short). PDS has the ability to launch defense projectiles from the space station headquarters (positioned at the center of the space station) to divert incoming attack projectiles (asteroids heading for Earth). Before the first firing of a projectile from the defense system, Aunt Entity would like to see a simulation showing how the incoming attack projectile's motion can be changed by the defense projectile to be sure that you can be trusted with the PDS.

• The mass of a defense projectile is about $20\,{\rm kg}$, made out of sticky Space Clay™.
• The average mass of an attack projectile is about $5$ times that of a defense projectile, usually made of a solid metallic material.

Complete the code below to simulate before and after an interception (collision) for a worst case scenario: an attack projectile being launched directly towards headquarters at its largest ever recorded velocity $\langle 225,-400,0 \rangle\,{\rm m/s}$ from its closest ever recorded position $\langle -500,900,0 \rangle\,{\rm m}$. For this worst case scenario defense to be successful, you must push the incoming attack projectile back along its incoming path so that its velocity is $\langle -450,800,0 \rangle\,{\rm m/s}$. Your code should be general enough to handle other attack and defense projectile initial conditions.

Furthermore, the Department of Projectile Energy (DoPE) for the Thunderdome would like a report on the loss of kinetic energy during the collision as it interested in further harnessing the power of the PDS once this asteroids problem is over. Use VPython's graphing capabilities to help answer how much energy is lost.