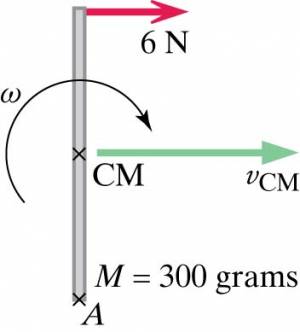
Consider a meter stick whose mass is 300 grams and that lies on ice (see representation in which we are looking down on the meter stick). You pull at one end of the meter stick, at right angles to the stick, with a force of 6 newtons. Assume that friction with the ice negligible. What is the rate of change of the center-of-mass speed $v_{CM}$? What is the rate of change of the angular speed $\omega$?

Mass of meter stick 300g

Pull at end of meter stick at right angles to the stick: 6N

Remember a meter stick is a meter long

Rate of change of the center-of-mass speed $v_{CM}$?

Rate of change of the angular speed $\omega$?

No friction due to ice

System: Stick

Surroundings: Your hand (pulling); ice (negligible effect)

$\frac{d\vec{P}}{dt}$ = $\vec{F}_{net}$

$\frac{d\vec{L}_{rot}}{dt}$ = $\vec{\tau}_{net,CM}$

$\tau = r_{A}Fsin \theta$

From the momentum principle:

$d\vec{P}/dt = d(m\vec{v}_{CM})/dt = \vec{F}_{net}$

$dv_{CM}/dt = (6N)/(0.3kg) = 20m/s^2$

Angular Momentum Principle about center of mass:

$d\vec{L}_{rot}/dt = \vec{\tau}_{net,CM}$

Component into screen (-z direction):

$Id\omega/dt = (0.5m)(6N)sin90^{\circ} = 3N \cdot m$

$d\omega/dt = (3N \cdot m)/[(0.3 kg \cdot m^2)/12] = 120 radians/s^2$

In vector terms, $d\vec{\omega}/dt$ points into the page, corresponding to the fact that the angular velocity points into the page and is increasing.