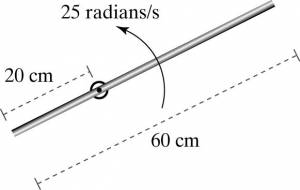
Example: A Rod Rotating Not Around Its Center
A thin rod with mass 140 grams and 60 cm long rotates at an angular speed of 25 radians/s about an axle that is 20cm from one end of the rod (see Figure in Representations). What is its kinetic energy?
Facts
Thin rod has a mass of 140 grams
Thin rod is 60 cm long
Thin rod rotates at an angular speed of 25 radians/s
Rotation occurs around an axle that is 20cm from one end of the rod
Assumptions and Approximations
The rod has to be sufficiently thin so your not worried about contributions to moment of inertia from parts that are far away.
Lacking
What is the kinetic energy of the rod?
Representations
$K_{tot} = K_{trans} + K_{rot} = \frac{1}{2}(Mr^{2}_{CM} + I_{CM})\omega^{2}$
$K_{trans} = \frac{1}{2}Mr^{2}_{CM}$
$K_{rot} = \frac{1}{2}I_{CM}\omega^{2}$
$I = (\frac{1}{12})ML^{2}$ for a thin rod
Solution
There is translational kinetic energy because the center of mass is moving, and there is rotational energy because there is rotation about the center of mass.
We know that $(r_{CM} = 0.1 m):$ because this the distance to the centre of mass from the point of rotation: (30cm - 20cm).
We are looking for the kinetic energy for a rigid body rotating about a point not the center of the mass.
The total energy has both translational and rotational components
$K_{tot} = K_{trans} + K_{rot}$
Substitute in equations for rotational kinetic energy and translational kinetic energy
$K_{tot} = \frac{1}{2}(Mr^{2}_{CM} + I_{CM})\omega^{2}$
Substitute in $(\frac{1}{12})ML^{2}$ for L as we are dealing with the inertia for a thin rod.
$K_{tot} = \frac{1}{2}(Mr^{2}_{CM}\;+\;\frac{1}{12}ML^{2})\omega^{2}$
Gather the M's out of both equations so that your equation now looks like:
$K_{tot} = \frac{1}{2}M(r^{2}_{CM}\;+\;\frac{1}{12}L^{2})\omega^{2}$
Insert values for the corresponding variables.
$K_{tot} = \frac{1}{2}(.140\;kg)((.1m^2)+\frac{1}{12}(.6m)^2)(25\;radians/s)^2$
Solve for $K_{tot}$
$K_{tot} = 1.75J$