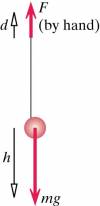
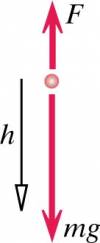
Example: A Yo-yo
You're playing with a yo-yo of mass m on a low-mass string (See Diagram in Representations). You pull up on the string with a force of magnitude F, and your hand moves up a distance d. During this time the mass falls a distance h (and some of the string reels off the yo-yo's axle).
(a) What is the change in translational kinetic energy of the yo-yo?
(b) What is the change in the rotational kinetic energy of the yo-yo, which spins faster?
Facts
a:
Initial State: Point particle with initial translational kinetic energy
Final State: Point particle with final translational kinetic energy
b:
Initial State: Initial rotational and translational kinetic energy
Final State: Final rotational and translational kinetic energy
Assumptions and Approximations
You are able to maintain constant force when pulling up on yo-yo
Assume no slipping of string around the axle. Spindle turns the same amount as string that has unravelled
No wobble included
String has no mass
Lacking
Change in translational kinetic energy of the yo-yo
Change in the rotational kinetic energy of the yo-yo
Representations
a:
Point Particle System
System: Point particle of mass $m$
Surroundings: Earth and hand
b:
Real system
System: Mass and string
Surroundings: Earth and hand
$\Delta K_{trans}$ = $\int_i^f \vec{F}_{net} \cdot d\vec{r}_{cm}$
$\Delta E_{sys}$ = $W_{surr}$
Solution
a:
From the Energy Principle ( when dealing with a point particle it only has $K_{trans}$):
$\Delta K_{trans}$ = $\int_i^f \vec{F}_{net} \cdot d\vec{r}_{cm}$
Substituting in for the forces acting on the yo-yo for $F_{net}$ and the change in position in the y direction for the centre of mass for $d\vec{r}_{cm}$ we get:
$\Delta K_{trans} = (F - mg)\Delta y_{CM}$
As indicated in diagram in the b section of the representation:
$\Delta y_{CM} = -h$
Substitute in $-h$ for $y_{CM}$
$\Delta K_{trans} = (F - mg)(-h)$
Multiply across by a minus and you get an equation for $\Delta K_{trans}$ that looks like:
$\Delta K_{trans} = (mg - F)h$
b:
From the energy principle we know:
$\Delta E_{sys}$ = $W_{surr}$
In this case we know that the change in energy in the system is due to the work done by the hand and the work done by the Earth.
$\Delta E_{sys} = W_{hand} + W_{Earth}$
Because we are dealing with the real system in this scenario the change in energy is equal to the change in translational kinetic energy + the change in rotational kinetic energy.
$\Delta K_{trans} + \Delta K_{rot} = W_{hand} + W_{Earth}$
Substitute in the work represented by force by distance for both the hand and the Earth.
$\Delta K_{trans} + \Delta K_{rot} = Fd + (-mg)(-h)$
From part (a) of the problem we can substitute in $(mg - F)h$ for $\Delta K_{trans}$ as the translational kinetic energy will be the same.
$\Delta K_{trans} = (mg - F)h$
Substituting this into our equation leaves us with:
$(mg - F)h + \Delta K_{rot} = Fd + mgh$
Solve for change in rotational kinetic energy:
$\Delta K_{rot} = F(d + h)$