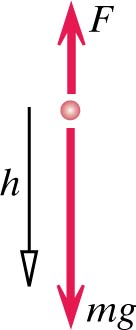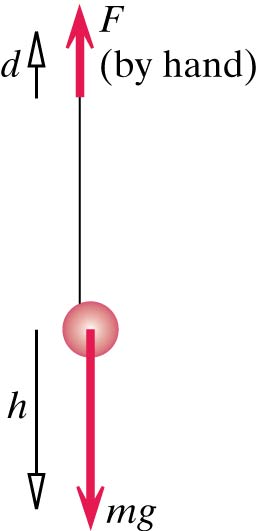
You're playing with a yo-yo of mass m on a low-mass string (See Diagram in Representations). You pull up on the string with a force of magnitude F, and your hand moves up a distance d. During this time the mass falls a distance h (and some of the string reels off the yo-yo's axle).

(a) What is the change in translational kinetic energy of the yo-yo?

(b) What is the change in the rotational kinetic energy of the yo-yo, which spins faster?

a:

Initial State: Point particle with initial translational kinetic energy

Final State: Point particle with final translational kinetic energy

b:

Initial State: Initial rotational and translational kinetic energy

Final State: Final rotational and translational kinetic energy

a:

Point Particle System

System: Point particle of mass $m$

Surroundings: Earth and hand

b:

Real system

System: Mass and string

Surroundings: Earth and hand

a:

From the Energy Principle (point particle only has $K_{trans}$):

$\Delta K_{trans} = (F - mg)\Delta y_{CM}$

$\Delta y_{CM} = -h (from\; digram)$

$\Delta K_{trans} = (F - mg)(-h) = (mg - F)h$

b:

$\Delta E_{sys} = W_{hand} + W_{Earth}$

$\Delta K_{trans} + \Delta K_{rot} = Fd + (-mg)(-h)$

$\Delta K_{trans} = (mg - F)h$ (From part (a))

$(mg - F)h + \Delta K_{rot} = Fd + mgh$

$\Delta K_{rot} = F(d + h)$