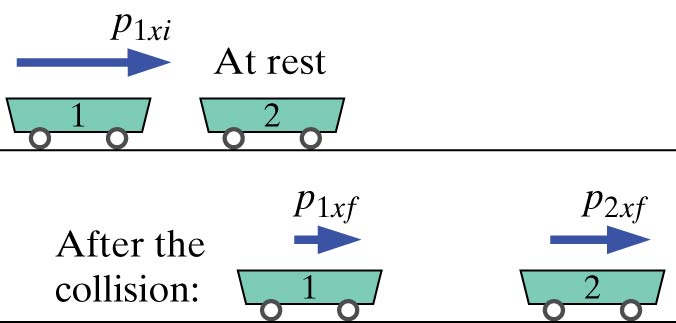
Cart 1 collides with stationary cart 2, which is identical. Suppose that the collision is (nearly) elastic, as it will be if the carts repel each other magnetically or interact through soft springs. In this case there is no change of internal energy. What are the final momenta of the two carts?

Cart 1 collides with Cart 2

Initial situation: Just before collision

Final situation: Just after collision

Final momenta of the two carts

Assume collision is elastic

Assume there is no change of internal energy

Neglect friction and air resistance - negligible effect of surroundings - only x components change

System: Both carts

Surroundings: Earth, track, air

$\vec{p}_f = \vec{p}_i + \vec{F}_{net} \Delta t$

$E_f = E_i + W + Q$

$K = \frac{1}{2}mv^{2}$

Since the y and z components of momentum don't change, we can work with only x components

From the momentum principle:

$$\vec{p}_f = \vec{p}_i + \vec{F}_{net} \Delta t$$

$$\vec{p}_{1xf} + \vec{p}_{2xf} = \vec{p}_{1xi} + 0$$

From the energy principle:

$$E_f = E_i + W + Q$$

$$K_{1f} + K_{2f} + E_{int1f} + E_{int2f} = K_{1i} + K_{2i} + E_{int1i} + E_{int2i}$$

$$K_{1f} + K_{2f} = K_{1i}$$

Combine momentum and energy equations:

$$\dfrac{p^{2}_{1xf}}{2m} + \dfrac{p^{2}_{2xf}}{2m} = \dfrac{(p_{1xf} + p_{2xf})^2}{2m}$$

$$p^{2}_{1xf} + p^{2}_{2xf} = p^{2}_{1xf} + 2{p_{1xf}p_{2xf}} + p^{2}_{2xf}$$

$$2{p_{1xf}p_{2xf}} = 0$$

There are two possible solutions to this equation. The term ${p_{1xf}p_{2xf}}$ can be zero if $p_{1xf} = 0$ or if $p_{2xf} = 0$.