Example: Predicting the location of an object undergoing constant force motion
The fan cart in the video below is observed to accelerate uniformly to the right. The air exerts a constant force on the blades that is around $0.45 N$. Determine the how far the fan cart has traveled after $2.2 s$ if the cart starts from rest.
Facts
- The fan cart accelerates uniformly to the right.
- The force by the air on the blades if $0.45 N$.
- The fan cart travels to the right for $2.2 s$.
- The fan cart starts from rest.
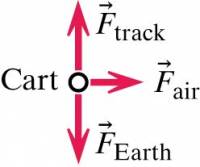
- The fan cart experiences several forces including:
- the force of the air on the blades (to the right)
- the gravitational force due to the interaction with the Earth (directly downward)
- the force applied by the track (directly upward)
- a frictional forces and air resistance that resist the motion
- The acceleration due to gravity is 9.8 $\dfrac{m}{s^2}$ and is directed downward.
Lacking
- The mass of the fan cart is not given, but can be found online ($m_{cart} = 0.3 kg$).
Approximations & Assumptions
- Over the interval that we care about it, we will assume the net force doesn't change. That is, the cart experiences constant force motion.
- As a result, the motion occurs only in the horizontal direction.
Representations
- The forces acting on the fan cart (the system's interactions with its surroundings) are represented in this free-body diagram.
- The net force acting on the fan cart is the sum of all the forces, $\vec{F}_{net} = \sum \vec{F}_i = \langle 0.45, 0, 0 \rangle N$.
- The displacement of the fan cart in the $x$-direction can be written like this: $x_{f} - x_{i} = v_{xi} \Delta t + \dfrac{1}{2}\dfrac{F_{net,x}}{m} \Delta t^2$
Solution
The displacement of the cart is given by,
$\Delta x_{cart} = x_{cart,f} - x_{cart,i} = v_{cart,xi} \Delta t + \dfrac{1}{2}\dfrac{F_{net,x}}{m_{cart}} \Delta t^2$
We can compute this displacement,
$$\Delta x_{cart} = (0 \dfrac{m}{s}) (2.2 s) + \dfrac{1}{2}\dfrac{0.45 N}{0.3kg}(2.2s)^2 = 3.6 m$$