Example: Predicting the final momentum & velocity using the Momentum Principle
Henrik Zetterberg is passing a hockey puck at a Red Wings practice. From video of the pass, you can determine the stick was in contact with the puck for $0.05 s$. You estimate the force with which “Zäta” passes the puck is about a tenth of his weight, so $100 N$. Determine how fast the puck leaves Zäta's stick.
Facts
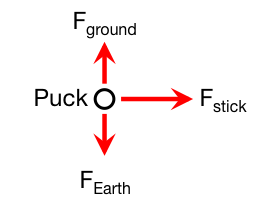
- The puck experiences several forces including
- the gravitational force (directly downward)
- the force of the stick
- the force due to the ice (upward)
- some frictional forces and air resistance
Lacking
- The mass of an NHL regulation hockey puck is unknown but can be found online ($m_{puck}=0.17kg$).
Approximations & Assumptions
- Over the time interval the puck is in contact with the stick, the frictional forces are negligible.
- The puck is contact with the stick for $0.05 s$.
- The force the stick exerts on the puck is roughly constant over the $0.05 s$ time interval.
- The force the stick exerts is $100 N$, and can be considered to act in a single direction.
- The puck starts from rest.
Representations
- The free-body diagram for this situation is given by the diagram below.
- The final momentum of the puck is given by the update form of the Momentum Principle: $\vec{p}_f = \vec{p}_i + \vec{F}_{net} \Delta t$.
Solution
Given the approximations and assumptions above, you can write the update form of the momentum principle for this question,
$$\vec{p}_f = m_{puck}\vec{v}_f = \vec{F}_{net} \Delta t$$
because the puck starts from rest. So that,
$$\vec{v}_f = \dfrac{\vec{F}_{net}}{m_{puck}} \Delta t$$
which we can consider in one dimension,
$$v_f = \dfrac{F_{net}}{m_{puck}} \Delta t = \dfrac{100 N}{0.17 kg}(0.05 s) = 29.4 \dfrac{m}{s}$$