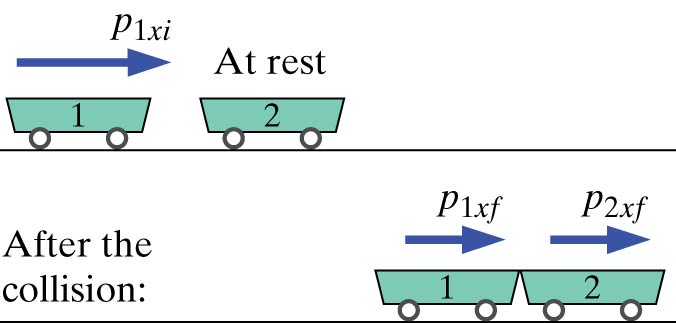
Example: Maximally Inelastic Collision of Two Identical Carts
Consider the opposite extreme - a maximally inelastic collision of the two identical carts, one initially at rest. That means the carts stick together (perhaps they have sticky material on their ends), and each has the same final momentum $p_{1xf} = p_{2xf}$
Find the final momentum, final speed, and final kinetic energy of the carts in terms of their initial values.
What is the change in internal energy of the two carts?
Facts
Initial situation: Just before collision
Final situation: Just after collision
Lacking
Find the final momentum, final speed, and final kinetic energy of the carts in terms of their initial values.
What is the change in internal energy of the two carts?
Approximations & Assumptions
External forces are negligible during the collision, so neglect friction and air resistance, which means the total momentum of the system is constant.
Representations
System: Both carts
Surroundings: Earth, track, air (neglect friction and air resistance)
$\vec{p}_f = \vec{p}_i + \vec{F}_{net} \Delta t$
$E_f = E_i + W + Q$
$K = \frac{1}{2}mv^{2} = \frac{1}{2}m(\frac{p}{m})^{2} = \frac{1}{2}m(\frac{p^{2}}{m})$
Solution
Since the y and z components of momentum don't change, we can work with only x components
From the momentum principle (x components) we know that the momentum before is equal to the momentum after:
$${p}_{1xf} + {p}_{2xf} = {p}_{1xi}$$
After the collision ${p}_{2xf}$ is equal to ${p}_{1xf}$ as they are stuck together so:
$$2p_{1xf} = p_{1xi}$$
Rearrange to isolate $p_{1xf}$
$$p_{1xf} = \dfrac{1}{2}p_{1xi}$$
Therefore the final speed of the stuck-together carts its half the initial speed:
$$v_{f} = \dfrac{1}{2}{v_{i}}$$
Since we know the speed of the carts we can calculate their translational kinetic energy.
Final translational kinetic energy is equal to twice the kinetic energy using the final velocity as $K_{1f} = K_{2f}$
$$(K_{1f} + K_{2f}) = 2(\dfrac{1}{2}mv^2_{f})$$
Substitute in the final speed of the stuck-together carts:
$$(K_{1f} + K_{2f}) = 2(\dfrac{1}{2}m(\dfrac{1}{2}v_{i})^2) = \dfrac{1}{4}mv^2_{i}$$
Substituting back in $K_{1i}$ in order to put the final kinetic energy in terms of the initial kinetic energy we get:
$$(K_{1f} + K_{2f}) = \dfrac{K_{1i}}{2}$$
We know the initial and final translational kinetic energies of the system, so we can use the energy principle to find the change in internal energy:
$$K_{1f} + K_{2f} + E_{int,f} = K_{1i} + E_{int,i}$$
Rearrange to get the final internal energy minus the initial internal energy one one side.
$$E_{int,f} - E_{int,i} = K_{1i} - (K_{1f} + K_{2f})$$
$E_{int,f} - E_{int,i}$ is the same as $\Delta E_{int}$ and this is what we are trying to find so substitute this in. Also substitute $\dfrac{K_{1i}}{2}$ for $(K_{1f} + K_{2f})$. We get:
$$\Delta E_{int} = K_{1i} - \dfrac{K_{1i}}{2}$$
Resolve the right hand side and you get:
$$\Delta E_{int} = \dfrac{K_{1i}}{2}$$
The final kinetic energy of the system is only half of the original kinetic energy, which means that the other half of the original kinetic energy has been dissipated into increased internal energy $\Delta E_{int}$ of the two carts.