Example: Calculating the net force

The fan cart is observed to experience a net force to the right.

Determine the (vector) net force acting on the fan cart.

You need to compute the net force on the fan cart using the information provided and any information that you can collect or assume.

• The fan cart accelerates to the right.
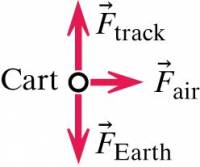
• The fan cart experiences several forces including:
  • the force of the air on the blades (to the right)
  • the gravitational force due to the interaction with the Earth (directly downward)
  • the force applied by the track (directly upward)
  • a frictional forces and air resistance that resist the motion
• The acceleration due to gravity is 9.8 $\dfrac{m}{s^2}$ and is directed downward.

• The mass of the fan cart is not given, but can be found online ($m_{cart} = 0.3 kg$).
• The force that the air exerts on the fan blades, which is responsible for the force to right, is unknown. This could be determined by finding the change in momentum of the fan cart over some time interval. Let's say that was done and it was found to be $F_{air} = 0.45 N$.

• Over the interval that we care about it, we will neglect the frictional forces and the force of air resistance.

• The net force acting on the fan cart is the sum of all the forces, $\vec{F}_{net} = \sum \vec{F}_i = \vec{F}_1 + \vec{F}_2 + \dots$.
• The forces acting on the fan cart (the system's interactions with its surroundings) are represented in this free-body diagram.

We simply compute the force vector noting that the momentum does not change in the vertical direction, so the forces on the cart due to gravity and the force on the cart due to the track are equal in magnitude.

The force on the cart due to the Earth is given by $F_{Earth} = m\vec{g}$ where $\vec{g} = \langle 0, -9.8, 0 \rangle \dfrac{m}{s^2}$. We compute,

$$F_{Earth} = m_{cart}\vec{g} = 0.3 kg\:\langle 0, -9.8, 0 \rangle \dfrac{m}{s^2} = \langle 0, -2.94, 0 \rangle N$$

So, we can now compute the net force,

$$\vec{F}_{net} = \sum \vec{F}_i = \vec{F}_{fan} + \vec{F}_{Earth} + \vec{F}_{track} = \langle 0.45, 0, 0 \rangle N + \langle 0, -2.94, 0 \rangle + \langle 0, 2.94, 0 \rangle = \langle 0.45, 0, 0 \rangle N$$

Notice this is simply the force that the air exerts on the blades. This is the force responsible for the momentum change of the fan cart.