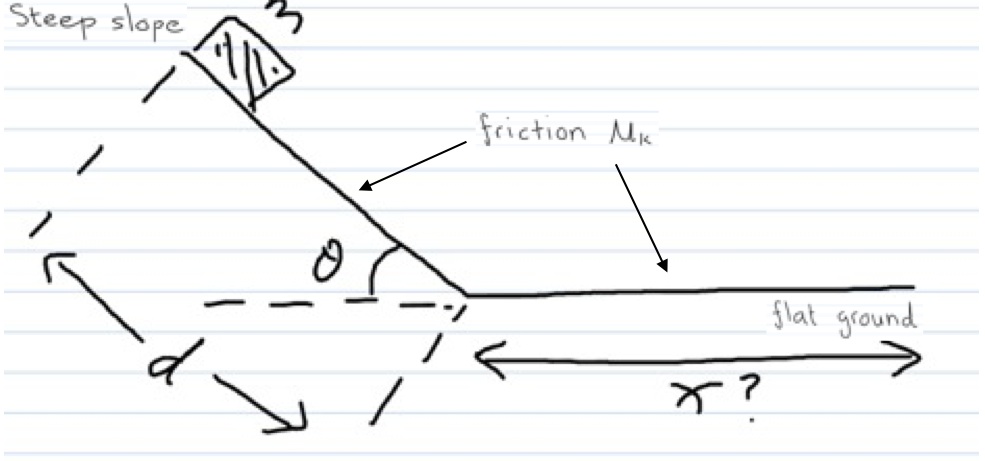
A little girl is riding her sled on a hill. If she starts a distance d up the hill, which makes an angle θ with the horizontal, how far will she travel along the flat snowy ground?

Child on incline of θ.

The total mass of the sled and child = m.

There's a small bit of friction between the rails of the sled and the snow = (μ_k).

Slope length = L

Initial state: at rest, at height above horizontal

Final state: at rest on horizontal

How far will she travel along the flat?

Coefficient for kinetic friction for flat + incline is the same.

No wind resistance.

System: Sled + Kid + Earth

Surroundings: Snow

$$\Delta E_{system} = W_{surroundings}$$

$$\Delta K + \Delta U_{g} = W_{friction}$$

$$\Delta E_{system} = W_{surroundings}$$

$$\Delta K + \Delta U_{g} = W_{friction}$$

no change

$$\Delta K = 0$$

$$\Delta U_{g} = W_{friction} \longrightarrow W_{friction}?$$

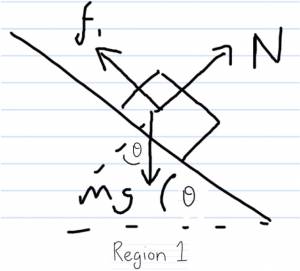
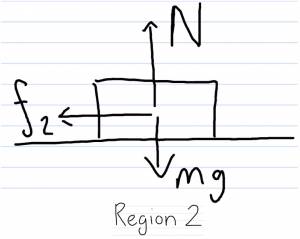
Here, we pause because we have two different regions to consider.

The frictional force is different in the two regions so we must consider the work they do separately.

$$\Delta U_{g} = W_{1} + W_{2}$$

$$\Delta U_{g} = \vec{f}_{1}\cdot\Delta \vec{r}_{1} + \vec{f}_{2}\cdot\Delta \vec{r}_{2}$$

$\vec{r}_{2}$ is what we care about. (position change along flat part)

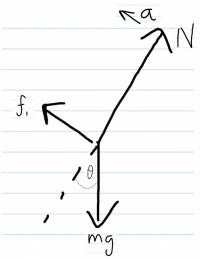
What's $f_{1}$ and $f_{2}?$

$\sum{F_{x}} = f_{1} - mgsinθ = ma_{1} \longrightarrow$ don't need this because $f_{1}=μ_{k}N$

$$\sum{F_{y}} = N - mgcosθ = 0$$

$$mgcosθ = N$$

$$f_{1} = μ_{k}mgcosθ$$

$$\sum{F_{x}} = f_{2} = ma_{2} \longrightarrow f_{2} = μ_{k}N = μ_{k}mg$$

$$\sum{F_{y}} = N-mg = 0$$

Again because not using kinematics we don't need accelerations.

$$\Delta U_{g} = \vec{f}_{1}\cdot\Delta \vec{r}_{1} + \vec{f}_{2}\cdot\Delta \vec{r}_{2}$$

In the previous equation $\vec{f}_{1}\cdot\Delta \vec{r}_{1} \longrightarrow W_{1}<0$ and $\vec{f}_{2}\cdot\Delta \vec{r}_{2} \longrightarrow W_{2}<0$ because $\vec{f}$'s are opposite to $\Delta \vec{r}$'s

$$\Delta U_{g} = -(μ_{k}mgcosθ)d - (μ_{k}mg)x$$

$$+mg(y_f - y_i) = -μ_{k}mgdcosθ - μ_{k}mgx$$

$$y_f - y_i = -μ_{k}(dcosθ + x)$$

What is $y_f-y_i$ in terms of what we know?

$$y_f-y_i = -dsinθ$$

$$-dsinθ = -μ_{k}(dcosθ + x)$$

$$dcosθ+x = \dfrac{d}{μ_{k}}sinθ$$

$$x = \dfrac{d}{μ_{k}}sinθ - dcosθ$$

$$x = d (\dfrac{sinθ-μ_{k}cosθ}{μ_{k}})$$

[x]=m

[d]=m

All other quantities are unitless.