This is an old revision of the document!
Example: The Jumper
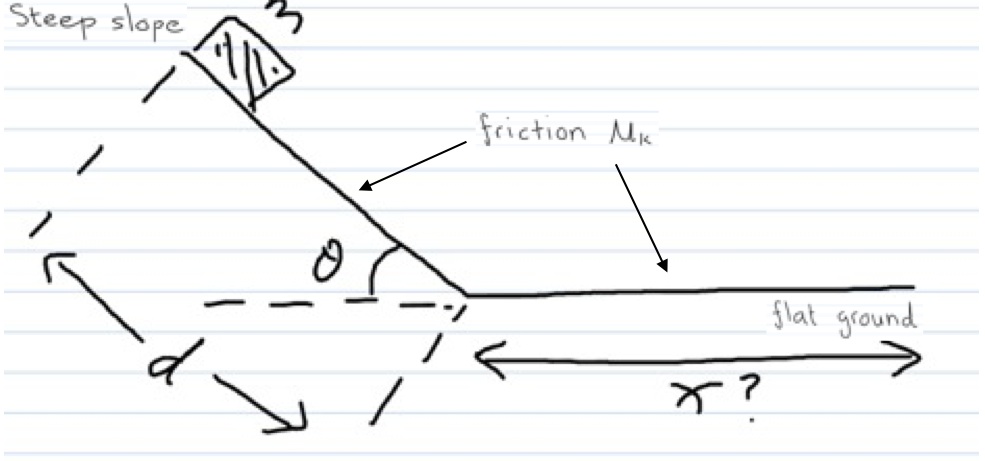
A little girl is riding her sled on a hill. If she starts a distance d up the hill, which makes an angle θ with the horizontal, how far will she travel along the flat snowy ground?
Facts
Child on incline of θ.
The total mass of the sled and child = m.
There's a small bit of friction between the rails of the sled and the snow = (μ_k).
Slope length = L
Initial state: at rest, at height above horizontal
Final state: at rest on horizontal
Lacking
How far will she travel along the flat?
Approximations & Assumptions
Coefficient for kinetic friction for flat + incline is the same.
No wind resistance.
Representations
Solution
ΔEsystem=Wsurroundings
ΔK+ΔUg=Wfriction
no change ΔK=0
ΔUg=Wfriction⟶Wfriction?
Here, we pause because we have two different regions to consider.
The frictional force is different in the two regions so we must consider the work they do separately.
ΔUg=W1+W2
ΔUg=→f1⋅Δ→r1+→f2⋅Δ→r2
→r2 is what we care about. (position change along flat part)
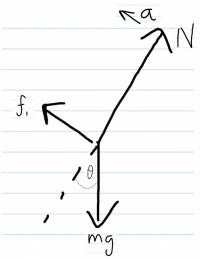
What's f1 and f2?
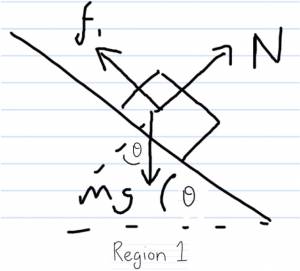
∑Fx=f1−mgsinθ=ma1⟶ don't need this because f1=μkN
∑Fy=N−mgcosθ=0
mgcosθ=N
f1=μkmgcosθ
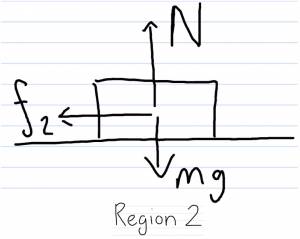
∑Fx=f2=ma2⟶f2=μkN=μkmg
∑Fy=N−mg=0
Again because not using kinematics we don't need accelerations.
ΔUg=→f1⋅Δ→r1+→f2⋅Δ→r2
In the previous equation →f1⋅Δ→r1⟶W1<0 and →f2⋅Δ→r2⟶W2<0 because →f's are opposite to Δ→r's
ΔUg=−(μkmgcosθ)d−(μkmg)x
+mg(yf−yi)=−μkmgdcosθ−μkmgx
yf−yi=−μk(dcosθ+x)
What is yf−yi in terms of what we know?
yf−yi=−dsinθ
−dsinθ=−μk(dcosθ+x)
dcosθ+x=dμksinθ
x=dμksinθ−dcosθ
x=d(sinθ−μkcosθμk)
[x]=m
[d]=m
All other quantities are unitless.