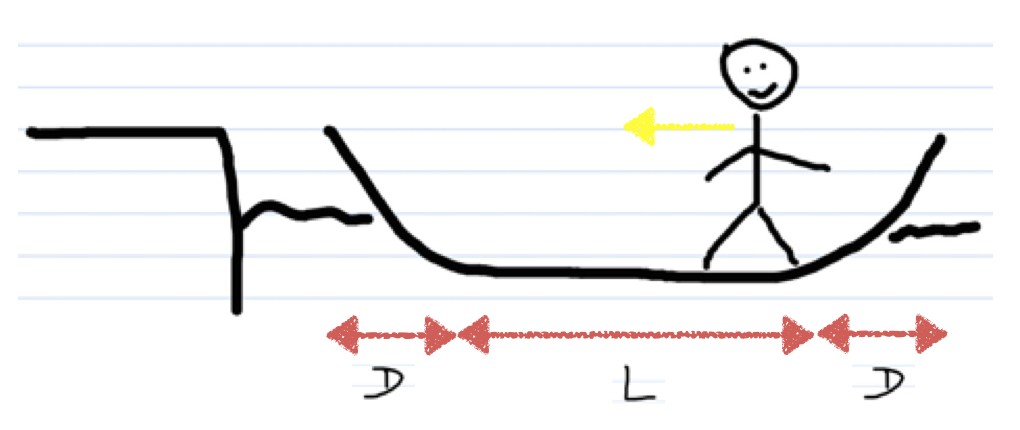
A person is standing in a boat that is a length 2D + L (see diagram). If they walk a distance L, how far is the boat from the dock?

Does the boat move L?

Boat Length: 2D + L

Mass person: m

Mass of boat: M

Initial Momentum: Everything at rest $\vec{p_i} = 0$

Final Momentum: Everything at rest $\vec{p_f} = 0$

System: Boat + Person

Surroundings: Nothing

How far is boat from dock after moving?

Neglect friction between the boat and the water.

$\Delta \vec{p}_{sys} = \vec{F}_{ext} \Delta t$

$\vec{p}_{sys,f} = \vec{p}_{sys,i}$

$\vec{r}_{cm} = \dfrac{1}{M_{tot}}\left(\sum_i m_i \vec{r}_i\right)$ in 1D

$\Delta \vec{p}_{sys} = \vec{F}_{ext} \Delta t$

$\Delta \vec{p}_{sys} = 0$

$\vec{p_{i}} = \vec{p_{f}}$

This means momentum is conserved and because $\vec{p_{i}} = \vec{p_{f}} = 0$ the center of the mass will not change its location. That is, the boat moves such that the center of mass is at the same location relative to the dock.

$\Delta \vec{p}_{sys} = 0 = M_{tot} \Delta \vec{v}{_{cm}} = 0$

$\Delta \vec{v}{_{cm}} = 0$

$\vec{v}{_{cm,i}} = \vec{v}{_{cm,f}}$

$\vec{r}{_{cm}}$ is fixed $\longrightarrow$ both are zero.

Initially,

$\vec{r}{_{cm}} = \dfrac{1}{M_{tot}}\left(\sum_i m_i \vec{r}_i\right)$ in 1D,

$x_{cm,i} = \dfrac {M(D+\dfrac{L}{2}) + m(D+L)}{M+m}$

In the final state, we don't know x, but we know that $x_{cm,f} = x_{cm,i}$ So we'll just use the unknown x.

$x_{cm,f} = \dfrac {M(x+D+\dfrac{L}{2}) + m(x+D)}{M+m}$

$x_{cm,f} = x_{cm,i}$

$\dfrac {M(x+D+\dfrac{L}{2}) + m(x+D)}{M+m} = \dfrac {M(D+\dfrac{L}{2}) + m(D+L)}{M+m}$

Same denominator

${M(x+D+\dfrac{L}{2}) + m(x+D)} = {M(D+\dfrac{L}{2}) + m(D+L)}$

Solve for x,

$M_x + M(D + \dfrac{L}{2}) + mx + mD = M(D+\dfrac{L}{2}) + mD + mL$

Cancel like terms

$Mx + mx = mL$

So,

$(M+m)x = mL$

$x = (\dfrac{m}{M+m})L$

This is how far the canoe is from the dock.

Does this make sense?

Units $(x) = m$ $(\dfrac{m}{M+m})$ = unitless

If M is really big then $x \equiv 0$, think oil thanker

$x = (\dfrac{m}{M+m})L \equiv \dfrac{m}{M}L \equiv 0$ when $M>>m$

If M = 0 then x $\equiv L$, no boat limit

$x = (\dfrac{m}{M+m})L \equiv \dfrac{m}{M}L \equiv L$ when $m>>M$

So the motion of the center of mass of a system is dictated by the net external force.