You have read that the moment of inertia for a system of discrete particles (that rotates about its center of mass) can be calculated by adding up the product of each mass and the square of the distance from the center of mass.

$$I = \sum_i m_i r_{\perp i}^2 = m_1 r_{\perp 1}^2 + m_2 r_{\perp 2}^2 + m_3 r_{\perp 3}^2 + \dots$$

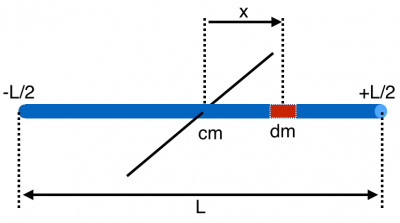
As you consider a continuous system where the particles cannot be discretized, but instead form a continuous system, the masses of the constant bits can be thought of as getting smaller and smaller. In this case, the sum becomes the integral over the whole system,

$$I = \int r^2\,dm$$

where $r^2$ is square of the magnitude of the vector that locates each bit of mass with respect to the rotation axis (typically, the center of mass). This is can be a difficult integral to perform and many tables of moments of inertia exist for typical geometric shapes and different centers of rotations. A fairly complete one appears here.