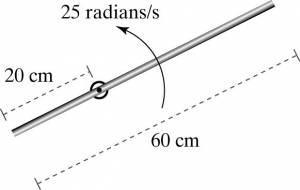
A thin rod with mass 140 grams and 60 cm long rotates at an angular speed of 25 radians/s about an axle that is 20cm from one end of the rod (see Figure in Representations). What is its kinetic energy?

Thin rod has a mass of 140 grams

Thin rod is 60 cm long

Thin rod rotates at an angular speed of 25 radians/s

Rotation occurs around an axle that is 20cm from one end of the rod

The rod has to be sufficiently thin so your not worried about contributions to moment of inertia from parts that are far away.

What is the kinetic energy of the rod?

$K_{tot} = K_{trans} + K_{rot} = \frac{1}{2}(Mr^{2}_{CM} + I_{CM})\omega^{2}$

$K_{trans} = \frac{1}{2}Mr^{2}_{CM}$

$K_{rot} = \frac{1}{2}I_{CM}\omega^{2}$

There is translational kinetic energy because the center of mass is moving, and there is rotational energy because there is rotation about the center of mass.

We know that $(r_{CM} = 0.1 m):$ because this the distance to the centre of mass from the point of rotation: (30cm - 20cm).

We are looking for the kinetic energy for a rigid body rotating about a point not the center of the mass.

The total energy has both translational and rotational components

$K_{tot} = K_{trans} + K_{rot}$

Substitute in equations for rotational kinetic energy and translational kinetic energy

$K_{tot} = \frac{1}{2}(Mr^{2}_{CM} + I_{CM})\omega^{2}$

$K_{tot} = \frac{1}{2}(Mr^{2}_{CM}\;+\;\frac{1}{12}ML^{2})\omega^{2}$

Gather the M's out of both equations so that your equation now looks like:

$K_{tot} = \frac{1}{2}M(r^{2}_{CM}\;+\;\frac{1}{12}L^{2})\omega^{2}$

Insert values for the corresponding variables.

$K_{tot} = \frac{1}{2}(.140\;kg)((.1m^2)+\frac{1}{12}(.6m)^2)(25\;radians/s)^2$

Solve for $K_{tot}$

$K_{tot} = 1.75J$