Formal derivation of $K_{trans}$ and $K_{rel}$
In the notes, you will read about the formal derivation to separate the total kinetic energy into a translational component that tracks the energy associated with the motion of the center of mass, and the relative component that that tracks the energy of due to the motion relative to the center of mass.
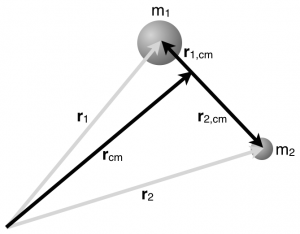
Locating objects relative to the center of mass
Begin by considering two particles, one of mass $m_1$ at location $\vec{r}_1$ measured relative to some fixed coordinate axes and the other of mass $m_2$ at location $\vec{r}_2$ measured relative to the same coordinate axes. Both of these vectors positions are indicated with grey arrows.
For these two particles, we could determine their center of mass,
$$\vec{r}_{cm} = \dfrac{m_1\,\vec{r}_1 + m_2\,\vec{r}_2}{m_1+m_2}$$
which is indicated by a black arrow, and then measure their positions relative to the center of mass ($\vec{r}_{1,cm}$ and $\vec{r}_{2,cm}$, also black arrows in the figure). The location of each particle can be related to these vectors,
$$\vec{r}_1 = \vec{r}_{cm} + \vec{r}_{1,cm} \qquad \vec{r}_2 = \vec{r}_{cm} + \vec{r}_{2,cm}$$
So in general you could have a collection of many particles each with a location vector given by,
$$\vec{r}_i = \vec{r}_{cm} + \vec{r}_{i,cm}$$
Total Kinetic Energy of a System of Particles
If you had a system of many particles, you could compute the total kinetic energy of the system by adding up the kinetic energy of each particle.
$$K_{tot} = \dfrac{1}{2}m_1\,v_1^2 + \dfrac{1}{2}m_2\,v_2^2 + \dfrac{1}{2}m_3\,v_3^2 + \dots$$
where the kinetic energy of the i-th particle is given by,
$$K_i = \dfrac{1}{2}m_i\,v_i^2$$
This kinetic energy is can be written in terms of the rate of change of the displacement of the particle,
$$K_i = \dfrac{1}{2}m_i\,\left[\dfrac{d\vec{r}_i}{dt}\right]^2$$ $$K_i = \dfrac{1}{2}m_i\,\left[\dfrac{d}{dt}\left(\vec{r}_{cm} + \vec{r}_{i,cm}\right)\right]^2 $$ $$K_i = \dfrac{1}{2}m_i\,\left[\dfrac{d\vec{r}_{cm}}{dt} + \dfrac{d\vec{r}_{i,cm}}{dt}\right]^2 $$ $$K_i = \dfrac{1}{2}m_i\,\left[\vec{v}_{cm} + \vec{v}_{i,cm}\right]^2 $$
where the last steps take into account the location with respect to the center of mass and result in separating the velocity of the particle into the sum of the velocity of the center of mass, and the velocity of the particle relative to the center of mass. This expression can be multiplied out using the dot product to find,
$$K_i = \dfrac{1}{2}m_i\,\left[\vec{v}_{cm}\cdot\vec{v}_{cm} + 2\vec{v}_{cm}\cdot\vec{v}_{i,cm} + \vec{v}_{i,cm}\cdot\vec{v}_{i,cm}\right] $$ $$K_i = \dfrac{1}{2}m_i\,\vec{v}_{cm}\cdot\vec{v}_{cm} + m_i\,\vec{v}_{cm}\cdot\vec{v}_{i,cm} + \dfrac{1}{2}m_i\,\vec{v}_{i,cm}\cdot\vec{v}_{i,cm}$$
And thus, the total kinetic energy is given by,
$$K_{tot} = \sum_i K_i = \underbrace{\sum_i \dfrac{1}{2}m_i\,\vec{v}_{cm}\cdot\vec{v}_{cm}}_{\mathrm{Term\;1}} + \underbrace{\sum_i m_i\,\vec{v}_{cm}\cdot\vec{v}_{i,cm}}_{\mathrm{Term\;2}}+ \underbrace{\sum_i \dfrac{1}{2}m_i\,\vec{v}_{i,cm}\cdot\vec{v}_{i,cm}}_{\mathrm{Term\;3}}$$
Through a bit more math, you will find that Term 1 is the translation kinetic energy of the center of mass and Term 3 is the relative kinetic energy. Term 2 turns out to be zero.
A Bit More Math
Term 1
In this first term, the only part that depends on the particle is the mass of the particle itself,
$$\sum_i \dfrac{1}{2}m_i\,\vec{v}_{cm}\cdot\vec{v}_{cm} = \dfrac{1}{2}\vec{v}_{cm}\cdot\vec{v}_{cm}\sum_i m_i = \dfrac{1}{2}M_{tot}\,v_{cm}^2$$
This is the translation kinetic energy of the center of mass of the system. All that matters for this term is the speed of the center of mass and the total mass of the system.
$$K_{trans} = \dfrac{1}{2}M_{tot}\,v_{cm}^2$$
Term 3
In this third term, each term in the sum involves the speed relative to the center of mass and the mass of each particle,
$$\sum_i \dfrac{1}{2}m_i\,\vec{v}_{i,cm}\cdot\vec{v}_{i,cm} = \sum_i \dfrac{1}{2}m_i\,v_{i,cm}^2$$
This sum cannot be cleaned up any more without knowing the relative speeds of the different terms in the sum. But this energy is precisely the energy due to motion relative to the center of mass because it uses the speeds relative to the center of mass of the system.
$$K_{rel} = \sum_i \dfrac{1}{2}m_i\,v_{i,cm}^2$$
Term 2
The second term is zero because of the definition of the center of mass.
$$\sum_i m_i\,\vec{v}_{cm}\cdot\vec{v}_{i,cm} = \vec{v}_{cm}\cdot\sum_i m_i\,\vec{v}_{i,cm} = \vec{v}_{cm}\cdot\sum_i m_i\,\dfrac{d\vec{r}_{i,cm}}{dt}$$
The term in the sum can be computed using the center of mass location vector,
$$\sum_i m_i\,\dfrac{d\vec{r}_{i,cm}}{dt} = \sum_i \dfrac{d}{dt}\left(m_i\,\vec{r}_{i,cm}\right) = \dfrac{d}{dt}\left( \sum_i m_i\,\vec{r}_{i,cm}\right)$$
where in the last step the fact that the sum of the derivative is the same as the derivative of the sum was used. The sum in bracket can be considered by itself and compared to the center of mass formula,
$$M_{tot}\vec{r}_{cm} = \sum_i m_i \vec{r}_i = \sum_i m_i \vec{r}_{cm} + \sum_i m_i \vec{r}_{i,cm}$$
The first term only depends on the total mass and is thus identical to the left hand side,
$$M_{tot}\vec{r}_{cm} = M_{tot}\vec{r}_{cm} + \underbrace{\sum_i m_i \vec{r}_{i,cm}}_{0\,\mathrm{for\;equality\;to\;hold}}$$
Hence,
$$\dfrac{d}{dt}\left( \sum_i m_i\,\vec{r}_{i,cm}\right) = 0$$
And therefore term 2 is precisely zero,
$$\sum_i m_i\,\vec{v}_{cm}\cdot\vec{v}_{i,cm} = 0$$