• What is a point particle system?
• What is a real system?
• What is vibrational energy?
• What is angular velocity?

Your success with the squirrel girl stuntwork has lead to your being hired by Marvel Entertainment again for the new Doctor Strange film. Benedict Cumberbatch is Doctor Stephen Vincent Strange, a neurosurgeon who protects the Earth from magical threats both foreign and domestic.

In one of the final scenes, Doctor Strange has been captured by Nightmare and has been sent to the Dark Dimension using a teleportation system constructed by Dormammu. The teleportation system is located on a small island above the Arctic circle. Ms. Marvel and Spiderman arrive to save Doctor Strange by crossing into the Dark Dimension. They find a sled that can be used to launch them into the teleportation system. Spidey uses his web shooters to attach a web strand to the teleportation system and accelerate he and Ms. Marvel into the teleportation system.

For this stunt, the current plan is to use a sled ($M_{\rm sled} = 1500\,{\rm kg}$) with a wire reel system attached to the front end. The wire will be attached to a snowmobile and the sled will be dragged across the ice while the wire unwinds from the reel. The sled must be traveling with a speed of 30 m/s at a distance of 100 m from its starting location.

Unfortunately, the island was chosen for its beauty and not any sort of safety considerations. The island itself is only 2.5 km across at its widest point, so the wire cannot unwind too much or the snowmobile will end up in the frozen arctic waters.

The reel is hoop-shaped, but its mass has not been chosen. Your team is meant to decide how to proceed with the stunt, and report back to the production company. Find the appropriate force that the snowmobile should exert on the wire/sled, and determine the mass of the reel. Some initial testing of reels of different masses and radii have shown (for a constant force) that the relationship between the angular speed of the reel and the linear speed of the sled is related to the ratio of the masses of the sled and reel. The equation that best fits this data is given below,

$$\omega_{\rm reel} = \dfrac{M_{\rm sled}}{m_{\rm reel}}\dfrac{v_{\rm sled}}{R_{\rm reel}}$$

Post-Solution questions:

1. If the reel tended to vibrate as it spun, how would you need to take this into account?
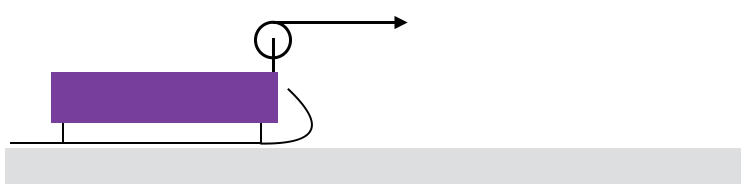
2. Consider a string pulling a rod on a frictionless surface. The string is attached to one end of the rod. If a constant force $F=10\,{\rm N}$ is applied completely horizontally, and your hand moves a distance $D=7\,{\rm m}$ while the center of mass moves a distance $d=5\,{\rm m}$. What is the rotational kinetic energy? Discuss the various ideas in this problem!
3. Qualitatively, draw a graph of what the velocities of the sled and the snowmobile look like as a function of time.
4. What is the maximum speed of the snowmobile and what is the power it delivers to the sled/reel system when moving at this maximum speed?
5. What design modifications could be made to this to make it more realistic?