Last time on post-apocalypse now: Your group of scientists have begun work on putting together an alternative power generator based on a merry-go-round ride from a playground. Suddenly a wormhole opens in the middle of the Thunderdome and four strangers clad in 2010's clothing emerge. They relay that they have been trapped for years in a place called the Marvel universe by someone named Korath and that they eventually escaped. Time does not flow at the same rate in the Marvel universe, and so they are shocked to find themselves in a post-apocalyptic Earth. They quickly develop a plan to rewrite history by combining the generator your scientists have been working on with exotic technology they stole from the Marvel universe to create a time machine that can send a small metallic item back in time. But first you need enough energy to power the time machine.

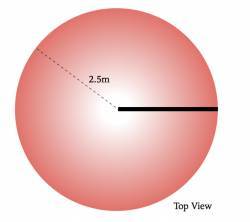
The merry-go-round ride has one bar moving from the centre of the ride to a point at the edge of the ride. You also have available to you seven 5kg weights with some straps. The uniform density disk that comprises the ride is 300kg and has a radius of 2.5m. Your team which is working on the roundabout consists of 4 members. You are informed by the lead scientist of the new arrivals “Flo Rida” that the ride needs to achieve an energy of either 1036 Joules or 6500 Joules in order to generate enough electricity to send what you have decided is a paperclip back in time.

But as plans are put in place the Thunderdome comes under attack from boar tigers. Luckily as a defensive precaution, a pit has been dug to surround the roundabout and been set on fire (boar-tigers are afraid of fire).

Powering the time machine to 1036 Joules will send the paperclip back to the original satellite launch and make critical machinery fail and stop the apocalypse. Powering the time machine to 6500 Joules will send the paper clip back to a time in which you knew Carver was driving his car before an accident and will cause the vehicle to explode preventing Carver from launching the satellite or any future satellites. The future (or the past) is in your hands. Choose wisely.

Turns out, you have access to a high-powered water hose of the kind typically used to fend off boar tigers! This may come in handy, as the rotating platform of the generator has small little cups which would act perfectly to catch water. The cups line the platform at a distance $r_{0}=2.5\,{\rm m}$ from the center, and the hose can generate a constant force $F_{0}=200\,{N}$.

In order to prove to Aunt Entity that this high-powered water hose is a much better approach to power the generator – since she cannot follow your mathematical acrobatics – you must produce a visual display of the angular momentum vector to demonstrate that the platform does indeed begin to speed up quickly.

But not too fast! As luck would have it, your water supply is limited! Determine how long it will take for the generator to ramp up to the required kinetic energy, using Python's graphing capabilities.

Attached below are the remnants of crazy Dr. Wiley's attempt at a simulation, however he just could not finish the job. Take up where he left off!

https://www.glowscript.org/#/user/paul.w.irving/folder/Public/program/YouSpinMeRightRoundPart2

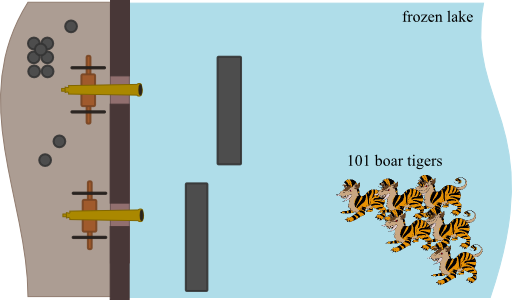
Your success at the Thunderdome command center has led to your being raised to the rank of subcommander in the Scorched Earth Army. You have been sent to a remote outpost in Icy Cape, Alaska. The outpost is the first line of defense against boar tigers for the rest of humanity. It is located at the shore of a large frozen lake across from which is the boar tiger breeding ground. The outpost was formerly a foundry for metal working; several large rectangular blocks (5 $\mathrm{m}$ wide; 1 $\mathrm{m}$ high; 1 $\mathrm{m}$ deep) of steel rest on the frozen lake. The blocks are not solid, but have a wall thickness of 10 $\mathrm{cm}$. The steel made at this foundry has a density of 7850 $\mathrm{kg/m^3}$.

Roving in packs of precisely 101, boar tiger hide cannot be penetrated by conventional weaponry (i.e., bullets and knives). During the last winter, the high commander of the outpost, Dr. Hodge, commissioned the deployment of cannons to defend the outpost. The cannons were engineered to fire .3 $\mathrm{m}$ diameter cannonballs at a speed of 1600 $\mathrm{m/s}$. These cannonballs are made of clay with a very thin steel shell ($m = 200 kg$). These were found to be ineffective against the packs of boar tigers resulting in many casualties. However, in that attack, Dr. Hodge observed that boar tigers were afraid of objects with swinging or sweeping motions.

Dr. Hodge has asked you to design a defense system that can defend against packs of boar tigers using the cannons (already in place) and the large, rectangular steel blocks. In his mind, it could be possible to have the steel blocks slide and rotate along the ice, sweeping up the attacking boar tigers along the way.

To determine if such a defense mechanism is feasible, Dr. Hodge requires that you determine how the steel block will move and with what speed it could be expected to strike boar tigers.