In general, any sort of flux is how much of something goes through an area. For example, we could think of a kid's bubble wand in terms of the air flux (from you blowing) through the circle (with the bubble solution in it). If you wanted to make bigger bubbles or make many more bubbles, you could do two things: increase the air flow or get a bubble wand with a bigger circle. Both of these actions (increasing the area and increasing the amount of air) will result in a larger “air flux” through the bubble wand. It's probably worth mentioning that we have assumed that you are holding the bubble wand so the circle is perpendicular to the air flow. If instead you rotate the wand 90 degrees, you will not get any bubbles since there is no air that is actually going through the circle part of the bubble wand. So the air flux not only depends on the amount of air and the area of circle, but also on how those two are oriented relative to each other. The idea of flux can be useful in many different contexts (i.e. fluids, electricity, air, etc.), but for any kind of flux, these are still the three conditions that matter: (1) the strength/amount, (2) the area, and (3) the orientation.

Electric flux then is the strength of the electric field on a surface area or rather the amount of the electric field that goes through an area. For electric flux, we need to consider: the strength of the electric field, the area that the field goes through, and the orientation of electric field relative to the area. These notes will introduce the mathematics behind electric flux, which we will use to build Gauss's Law.

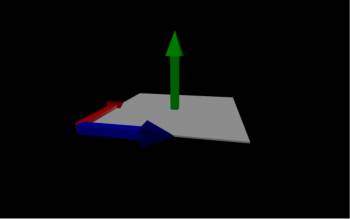
To start, we need to be able to describe how a surface area is oriented relative to the electric field. When we are talking about orientation in space, we are inherently talking about directions, so making use of vectors here would make sense. If we want to describe the area of a piece of paper that is laying flat on the table, we could say it has a length of 10 cm in the $\hat{x}$ direction (shown by the blue arrow) and a width of 12 cm in the $\hat{y}$ direction (shown by the red arrow). This is enough information for anyone to be able to tell how the paper is oriented on the table; however, to get the area of the paper, we need to take the length times the width, which gets tricky because length and width are now vectors. Because we want to keep the information about the direction, we should use the cross product to find the area in terms of a vector:

$$\vec{A}=\vec{l} \times \vec{w}$$ where $\vec{A}$ is the area vector, $\vec{l}$ is the length vector ($\vec{l}=10 \hat{x}$), and $\vec{w}$ is the width vector ($\vec{w}=12 \hat{y}$). Using the cross product formula, we get $$\vec{A}=\langle 10, 0,0 \rangle \times \langle 0,12, 0 \rangle$$ $$\vec{A}=\hat{x}(0*0-12*0)-\hat{y}(10*0-0*0)+\hat{z}(10*12-0*0)$$ $$\vec{A}=10*12 \hat{z}=|\vec{l}||\vec{w}|\hat{z}$$ $$\vec{A}=120 cm^2 \hat{z}$$ This result tells us that the area vector has a magnitude of length times width (just like normal for a rectangle) and has a direction in $\hat{z}$ direction, which is perpendicular to the piece of paper (shown by the green arrow). This is particularly useful because we now have a way to describe the area in terms of a single vector (that points perpendicular to the area) rather than dealing with two vectors (like length and width).

If instead, we rotate the piece of paper so that the short edge is resting on the table, then the length would be given as $\vec{l}=10\hat{y}$ but now the width is in the $\hat{z}$ direction. If we wanted to describe the area of the paper now, it would be:

$$\vec{A}=\langle 0, 0,12 \rangle \times \langle 0,10, 0 \rangle$$ which if you calculate the cross product, will give: $$\vec{A}=12*10 \hat{x}$$ $$\vec{A}=120 cm^2 \hat{x}$$ In this case, we get that the area is the same but the direction that the area vector points has changed. This is good because we didn't tear the piece of paper in half or change its size, we only rotated the piece paper. Again, we still have the magnitude of the area vector is equal to the area of the piece of paper, and the direction of the area vector points perpendicular to the surface.

It turns out that this result is fairly generalizable - the magnitude of the area vector is the equal to the area of the surface, while the direction points perpendicular to the surface. We can use this rule as a shortcut to writing the area vector rather than calculating a cross product every time (though the cross product method will always work).

Now that we have a way to write area as a vector, we can start to write out the equation for electric flux. To start, we will make two simplifying assumptions: the area is flat and the electric field is constant (in magnitude and direction). Later, we will relax these assumptions to deal with more complicated situations, but for now, we will start with the most simple case.

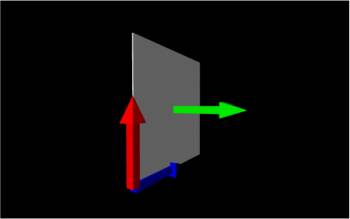
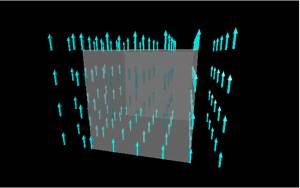
Let's say we have a constant electric field that points straight up (shown by the blue arrows) through a flat sheet (shown in grey - extends in the xz-plane). For this situation, we would write the area vector of the sheet as $\vec{A}=A_{sheet}\hat{y}$ (shown by the red arrow) and the electric field as $\vec{E}=E \hat{y}$. When the area vector is parallel to electric field, we would have the maximum electric flux possible (all of the electric field vectors go through the sheet).

If instead we rotate the area so that $\vec{A}=A_{sheet}\hat{x}$, then $\vec{A}$ (shown in green) is perpendicular to $\vec{E}$ (shown in blue) and none of the electric field vectors go through the sheet. In this case, the electric flux would be zero, even though we did not change anything about the electric field or area other than the orientation. This means, mathematically, we need a way to tell if the electric field is parallel to the area vector - or really we need a way to tell how much of the electric field is parallel to the area vector. This is what the dot product is used for - picking out how much of one vector points in the direction of another.

Thus, we can write the electric flux for a constant electric field through a flat area as:

$$\Phi_e=\vec{E} \bullet \vec{A}$$ where $\vec{E}$ is the electric field vector, $\vec{A}$ is the area vector, and $\Phi_e$ is the electric flux. Note that because of the dot product, electric flux is a scalar number (it has no direction). Electric flux will be positive if the area and electric field vectors point in the same direction or it will negative if they point in the opposite direction. The units of electric flux would be the units of electric field time the units of area so $\frac{N}{C}m^2$ or $\frac{V}{m}m^2=Vm$. We could also simplify the dot product by using the angle between the two vectors ($\vec{E}$ and $\vec{A}$ in this case): $$\Phi_e=\vec{E} \bullet \vec{A}=|\vec{E}||\vec{A}|cos(\theta)$$

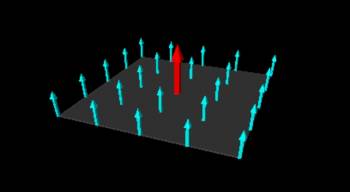
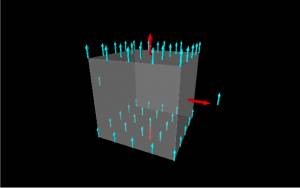
Now let's say we have a hollow cube as a surface (with each side having a length of $d$) that is placed in the same constant electric field. What would be the electric flux through the cube?

To find the total electric flux through the cube, we need to find the electric flux through each surface. By convention, we assume that the area vector(s) points out of the surface when you have a closed shape. (There is not really a justification as to why we pick the area vector(s) to point outward, other than it is a consistent way to define the shape.) For a cube, then we need to find the electric flux through 6 surfaces: the top of the cube, the bottom of the cube, and the four sides of the cube.

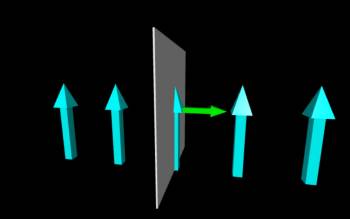
If we start with the right side of the cube, then we know the electric field points up (in $+\hat{y}$ direction) and the area vector should point perpendicular to the right side (shown by the red arrow), which in this case would be the $+\hat{x}$ direction. We can write the electric flux through the right side then as:

$$\Phi_{right}=E\hat{y} \cdot d^2 \hat{x}=Ed^2 \hat{y} \cdot \hat{x}$$ Because $\hat{y}$ and $\hat{x}$ are perpendicular, $\hat{y} \cdot \hat{x}=0$. Another way of thinking of this would be: $$\Phi_{right}=E\hat{y} \cdot d^2 \hat{x}=Ed^2 cos(\theta)$$ Because the area vector and the electric field vector are perpendicular, this means that $\theta=90$ so $cos(90)=0$. Both of these methods so that the electric flux through the right side is zero. If we draw out the electric field vectors, none of them would point through the right surface, so: $$\Phi_{right}=0$$ This would be true for all the sides of the cube - no field vectors point through the sides (the area vectors on the sides are all perpendicular to the electric field). So there is no electric flux through any of the sides: $$\Phi_{right}=\Phi_{left}=\Phi_{front}=\Phi_{back}=0$$

This leaves the top and bottom surfaces that we need to find the flux through. For the top surface, the area vector will point in $+\hat{y}$ direction (shown by the top red arrow), so $\vec{A}_{top}=d^2\hat{y}$. The flux through the top is then:

$$\Phi_{top}=\vec{E} \hat{y} \cdot d^2 \hat{y}=Ed^2 \hat{y} \cdot \hat{y}$$ Since $\vec{E}$ and $\vec{A}$ point in the same direction, $\hat{y} \cdot \hat{y}=1$, so $$\Phi_{top}=Ed^2$$ Finally, for the bottom surface, we still have $\vec{E}=E\hat{y}$ but now the area vector will point down because the area vector should point towards the outside of the cube (shown by the bottom red arrow). Remember, this is because the convention for closed surfaces is that area vectors point outward from the surface. This means that the area vector for the bottom surface is given by $\vec{A}=-d^2\hat{y}$. So the flux for the bottom surface is given by: $$\Phi_{bottom}=\vec{E} \cdot \vec{A}=E \hat{y} \cdot -d^2\hat{y}$$ $$\Phi_{bottom}=-Ed^2 \hat{y} \cdot \hat{y}$$ $$\Phi_{bottom}=-Ed^2$$ So the flux through the bottom of the cube is the same as the flux through the top but negative in sign because the electric field and the area vectors are anti-parallel on the bottom surface.

The total electric flux for the cube then is sum of the electric flux through each surface:

$$\Phi_{tot}=\Phi_{right}+\Phi_{left}+\Phi_{front}+\Phi_{back}+\Phi_{top}+\Phi_{bottom}$$ $$\Phi_{tot}=0+0+0+0+Ed^2-Ed^2$$ $$\Phi_{tot}=0$$ Even though there are field vectors that go through the top and bottom surfaces, the total electric flux through the cube is zero because there is just as much electric flux going “out” of the cube (through the top surface) and there is going “into” the cube (through the bottom surface). As you will see, this indicates there's no net charge in the cube.

• Flux through a Tilted Surface
  • Video Example: Flux through a Tilted Surface
• Flux through a Closed Cylinder