Suppose you have a circular ring, in which which there is a current $I$. The radius of the ring is $R$. The current produces a magnetic field. What is the magnetic field at the center of the ring?

• The current in the ring is $I$.
• The radius of the ring is $R$.

• $\vec{B}$

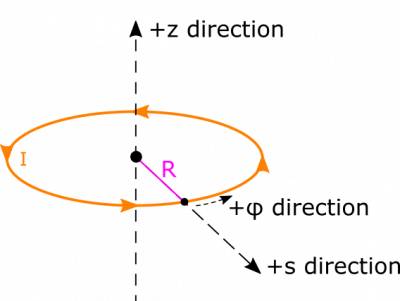
• If we orient the ring in the $xy$-plane and look down, the current flows in the counterclockwise direction.
• The current is steady.
• There are no other contributions to the magnetic field.

• We represent the Biot-Savart Law for magnetic field from a current as

$$\vec{B} = \int \frac{\mu_0}{4 \pi}\frac{I \cdot d\vec{l}\times \vec{r}}{r^3}$$

• We represent the situation below. We put the center of the ring at the origin. We choose cylindrical coordinates because we will be integrating over the length of the ring, and being able to represent its radius as constant will simplify calculations.

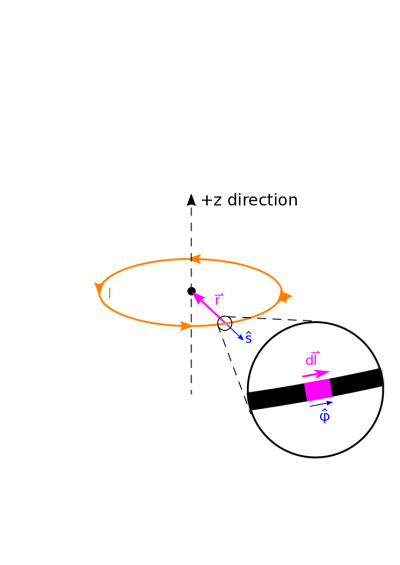
Below, we show a diagram with a lot of pieces of the Biot-Savart Law unpacked. We show an example $\text{d}\vec{l}$, and a separation vector $\vec{r}$. Notice that $\text{d}\vec{l}$ is directed along the segment, in the same direction as the current. The separation vector $\vec{r}$ points as always from source to observation.

Let's start breaking down some of the components of the Biot-Savart Law we listed in our representations. We can say for now that $\text{d}\vec{l}$ is directed in the $\hat{\phi}$ direction. The length of our $\text{d}\vec{l}$ is $R\text{d}\phi$ which comes from the arc length formula. We can therefore write $$\text{d}\vec{l} = R\text{d}\phi\hat{\phi}$$

We also represent the separation vector using a cylindrical unit vector, too: $$\vec{r} = \vec{r}_{\text{obs}} - \vec{r}_{\text{source}} = 0 - R\hat{s} = -R\hat{s}$$

Now, we combined the two vectors in their cross product: $$\text{d}\vec{l} \times \vec{r} = (R\text{d}\phi\hat{\phi}) \times (-R\hat{s}) = R^2 \text{d}\phi (-\hat{\phi} \times \hat{s}) = R^2 \text{d}\phi \hat{z}$$

Notice that even though the direction of $\hat{\phi}$ and $\hat{s}$ depend on the angle $\phi$ at which the vectors exist, their cross product, $\hat{z}$, does not depend at all on $\phi$. This will greatly simplify our integration later.

For now, we write $$\text{d}\vec{l} = \langle \text{d}x, \text{d}y, 0 \rangle$$ and $$\vec{r} = \vec{r}_{obs} - \vec{r}_{source} = 0 - \langle x, y, 0 \rangle = \langle -x, -y, 0 \rangle$$ Notice that we can rewrite $y$ as $y=-L-x$. This is a little tricky to arrive at, but is necessary to figure out unless you rotate your coordinate axes, which would be an alternative solution to this example. If finding $y$ is troublesome, it may be helpful to rotate. We can take the derivative of both sides to find $\text{d}y=-\text{d}x$. We can now plug in to express $\text{d}\vec{l}$ and $\vec{r}$ in terms of $x$ and $\text{d}x$: $$\text{d}\vec{l} = \langle \text{d}x, -\text{d}x, 0 \rangle$$ $$\vec{r} = \langle -x, L+x, 0 \rangle$$ Now, a couple other quantities that we see will be useful: $$\text{d}\vec{l} \times \vec{r} = \langle 0, 0, \text{d}x(L+x) - (-\text{d}x)(-x) \rangle = \langle 0, 0, L\text{d}x \rangle = L\text{d}x \hat{z}$$ $$r^3 = (x^2 + (L+x)^2)^{3/2}$$ The last thing we need is the bounds on our integral. Our variable of integration is $x$, since we chose to express everything in terms of $x$ and $\text{d}x$. Our segment begins at $x=-L$, and ends at $x=0$, so these will be the limits on our integral. Below, we write the integral all set up, and then we evaluate using some assistance some Wolfram Alpha. $$\begin{align*} \vec{B} &= \int \frac{\mu_0}{4 \pi}\frac{I \cdot d\vec{l}\times \vec{r}}{r^3} \\ &= \int_{-L}^0 \frac{\mu_0}{4 \pi}\frac{IL\text{d}x}{(x^2 + (L+x)^2)^{3/2}}\hat{z} \\ &= \frac{\mu_0}{2 \pi}\frac{I}{L}\hat{z} \end{align*}$$