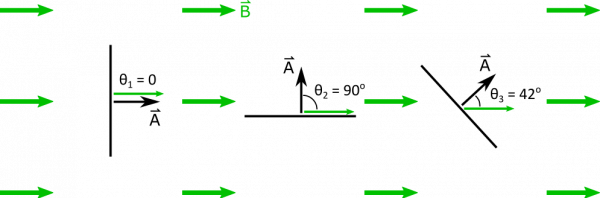
Suppose you have a magnetic field $\vec{B} = 0.6 \text{ mT } \hat{x}$. Three identical square loops with side lengths $L = 0.5 \text{ m}$ are situated as shown below. The perspective shows a side view of the square loops, so they appear very thin even though they are squares when viewed face on.

• The orientations of the square loops are as indicated above. They can be described by their angles with respect to the magnetic field. $\theta_1 = 0$, $\theta_2 = 90^\text{o}$, $\theta_3 = 42^\text{o}$.
• The magnetic field is $\vec{B} = 0.6 \text{ mT } \hat{x}$.
• The length of a square's side is $L = 0.5 \text{ m}$.

• The magnetic flux through each loop.

• The loops have flat faces.
• The magnetic field does not change with time, and is uniform in space.

• We represent magnetic flux through an area as

$$\Phi_B = \int \vec{B} \bullet \text{d}\vec{A}$$

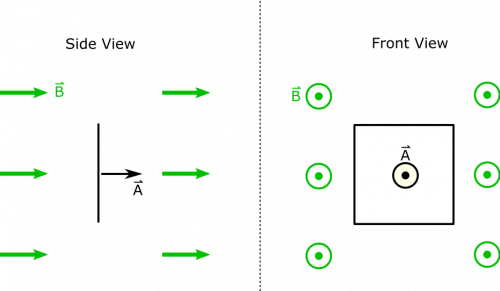
• We represent the situation with the given representation in the example statement above. Below, we also show a side and front view of the first loop for clarity.

Since the magnetic field has a uniform direction, and the area of the loop is flat (meaning $\text{d}\vec{A}$ does not change direction either), then we can simplify the dot product:

$$\vec{B} \bullet \text{d}\vec{A} = B\text{d}A\cos\theta$$

Since $B$ and $\theta$ do not change for different little pieces ($\text{d}A$) of the area, we can pull them outside the integral:

$$\int B\text{d}A\cos\theta =B\cos\theta \int \text{d}A = BA\cos\theta$$

Area for a square is just $A = L^2$, and $\theta$ is different for each loop:

$$\Phi_B = \begin{cases} BL^2\cos 0 = 1.5 \cdot 10^{-4} \text{ Tm}^2 & \text{Loop 1} \\ BL^2\cos 90^\text{o} = 0 & \text{Loop 2} \\ BL^2\cos 42^\text{o} = 1.1 \cdot 10^{-4} \text{ Tm}^2 & \text{Loop 3} \end{cases}$$

Notice that we could've given answers for Loops 1 and 2 pretty quickly, since they are parallel and perpendicular to the magnetic field, respectively, which both simplify the flux calculation greatly.