Two parallel wires have currents in opposite directions, $I_1$ and $I_2$. They are situated a distance $R$ from one another. What is the force per length $L$ of one wire on the other?

• $I_1$ and $I_2$ exist in opposite directions.
• The two wires are separated by a distance $R$.

• $\frac{\vec{F}}{L}$

• The currents are steady.
• The wires are infinitely long.
• There are no outside forces to consider.

• We represent the magnetic field from a very long wire as

$$\vec{B}=\frac{\mu_0 I}{2 \pi r} \hat{z}$$

• We represent the magnetic force on a little piece of current as

$$\text{d}\vec{F}= I \text{d}\vec{l} \times \vec{B}$$

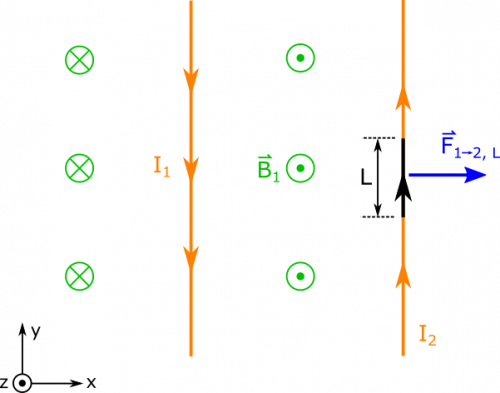
• We represent the situation with diagram below.

We know that the magnetic field at the location of Wire 2 from Wire 1 is given by the magnetic field of a long wire: $$\vec{B}_1=\frac{\mu_0 I_1}{2 \pi r} \hat{z}$$

We can reason that the direction of the field is $+\hat{z}$ because of the Right Hand Rule. We also don't care about the magnetic field from Wire 2 at the location of Wire 2, since Wire 2 cannot exert a force on itself. Now, it remains to calculate the magnetic force.

Since we know the magnetic field, the next thing we wish to define is $\text{d}\vec{l}$. Wire 2 has current directed with $\hat{y}$ in our representation, so we can say $$\text{d}\vec{l} = \text{d}y \hat{y}$$

This gives $$\text{d}\vec{l} \times \vec{B}_1 = \frac{\mu_0 I_1}{2 \pi r}\text{d}y \hat{x}$$

Lastly, we need to choose the limits on our integral. We can select our origin conveniently so that the segment of interest extends from $y=0$ to $y=L$. Now, we write:

$$\frac{\vec{F}_{1 \rightarrow 2}}{L} = \int_0^L I_2 \text{d}\vec{l} \times \vec{B}_1 = \int_0^L \frac{\mu_0 I_1 I_2}{2 \pi r}\text{d}y \hat{x} = \frac{\mu_0 I_1 I_2 L}{2 \pi r} \hat{x}$$