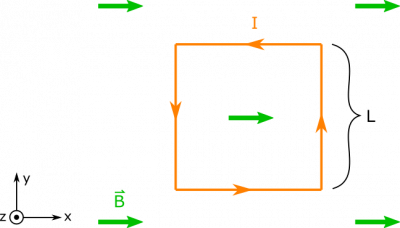
Suppose you have a square loop (side length $L$) of current $I$ situated in a uniform magnetic field $\vec{B}$ so that the magnetic field is parallel to two sides of the loop. What is the magnetic force on the loop of current?

• The loop is a square with side-length $L$.
• The magnetic field is parallel to two sides of the loop, and has a magnitude $B$.
• The current in the loop is $I$.

• The magnetic force on the loop.

• The current is in a steady state.
• The magnetic field does not change.
• There are no outside forces to consider.

• We represent the magnitude of force on a current-carrying wire in a magnetic field as

$$\left| \vec{F} \right|=IBL\sin\theta$$

• We represent the situation with the diagram below.

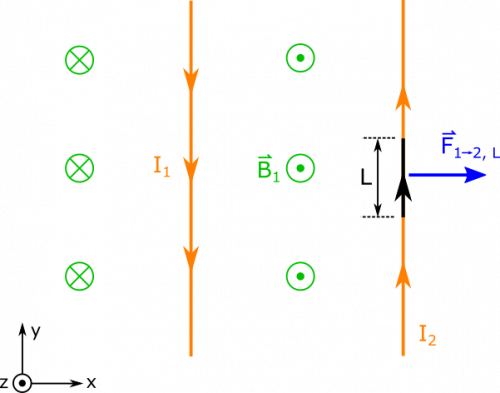
We know that the magnetic field at the location of Wire 2 from Wire 1 is given by the magnetic field of a long wire:

$$\vec{B}_1=\frac{\mu_0 I_1}{2 \pi r} \hat{z}$$

We can reason that the direction of the field is $+\hat{z}$ because of the Right Hand Rule. We also don't care about the magnetic field from Wire 2 at the location of Wire 2, since Wire 2 cannot exert a force on itself. Now, it remains to calculate the magnetic force.

Since we know the magnetic field, the next thing we wish to define is $\text{d}\vec{l}$. Wire 2 has current directed with $\hat{y}$ in our representation, so we can say

$$\text{d}\vec{l} = \text{d}y \hat{y}$$

This gives

$$\text{d}\vec{l} \times \vec{B}_1 = \frac{\mu_0 I_1}{2 \pi r}\text{d}y \hat{x}$$

Lastly, we need to choose the limits on our integral. We can select our origin conveniently so that the segment of interest extends from $y=0$ to $y=L$. Now, we write:

$$\vec{F}_{1 \rightarrow 2 \text{, L}} = \int_0^L I_2 \text{d}\vec{l} \times \vec{B}_1 = \int_0^L \frac{\mu_0 I_1 I_2}{2 \pi r}\text{d}y \hat{x} = \frac{\mu_0 I_1 I_2 L}{2 \pi r} \hat{x}$$

Notice that this force is repellent. The equal and opposite force of Wire 2 upon Wire 1 would also be repellent. Had the two current been going in the same direction, one can imagine that the two wires would attract each other.