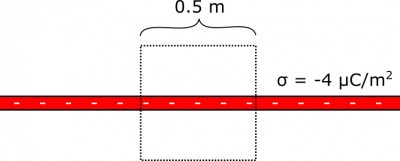
Suppose you have a plane of charge with uniform surface charge density of $\sigma=-4\mu\text{C/m}^2$. What is the electric flux through a cube with side-length $0.5 \text{ m}$ that is placed halfway into the plane? Feel free to use the electric field due to an infinite uniform plane of charge: $\vec{E} = \frac{\sigma}{2\epsilon_0}(\pm\hat{z})$ (where $\pm\hat{z}$ points away from plane). Notice that the strength of the electric field does not depend on the distance from the plane – it is constant apart from a change in direction when you cross over to the other side of the plane.

• The cube has side-length $q=1 \text{0.5 m}$.
• The cube is halfway into the plane – presumably this means the plane bisects the cube.
• The plane has surface charge density $\sigma=-4\mu\text{C/m}^2$.

• $\Phi_e$ for the cube.

• There are no other charges that contribute appreciably to the flux calculation.
• The cube is aligned with respect to the plane so that all its faces are either parallel or perpendicular to the plane.

• We represent the electric flux through a surface with:

$$\Phi_e=\int\vec{E}\bullet \text{d}\vec{A}$$

• We represent the electric field due to a plane of uniform surface charge density with:

$$\vec{E} = \frac{\sigma}{2\epsilon_0}(\pm\hat{z})$$

• We represent the situation with the following diagram.

First, we evaluate the situation qualitatively. Consider the electric field lines of the charged plane: You might notice that we have oriented the cube conveniently. The electric field is parallel to the sides of the cube, so there are no electric field lines entering or exiting from the side of the cube. So the flux through the sides should be $0$. For the top and bottom of the cube, the electric field lines are perpendicular to the surface, which means they are parallel to the area-vectors. These facts will greatly simplify our integral calculation of the flux. $$\Phi$$

You can imagine that if we were able to draw this in three dimensions, we would have just as many field lines entering the cylinder as exiting. Since flux is a measure of the “flow” of electric field through a surface, we could say that the flux is zero: the inward flow cancels with the outward flow. For now, we tentatively write: $$\Phi_{\text{cylinder}}=0$$ We gain more confidence when we read the next section of notes, where we define “Gauss' Law”. This law states that the total flux through a close surface is the amount of charge divided by $\epsilon_0$, the permittivity of free space. $$\Phi_{\text{total}}=\int \vec{E} \cdot \text{d}\vec{A}=\frac{Q_{\text{enclosed}}}{\epsilon_0}$$ Since the total charge of the dipole is $0$, then indeed the charge enclosed is $0$, and we were correct with our reasoning about the electric field and flux above.