Suppose you have a line of charge with a uniform linear charge density of $\lambda=15\mu\text{C/m}$. What is the electric flux through a cylinder with radius $R=0.5 \text{ m}$, and length $l=3 \text{ m}$ that is placed so that its axis is aligned with the line of charge? Feel free to use the electric field due to an infinite uniform line of charge: $\vec{E} = \frac{\lambda}{2\pi r\epsilon_0}\hat{r}$ (where $\hat{r}$ points away from line, and $r$ is the distance from the line).

• The cylinder has radius $R=0.5 \text{ m}$, and length $l=3 \text{ m}$.
• The axis of the cylinder is aligned with the line charge.
• The line charge has linear charge density $\lambda=15\mu\text{C/m}$.

• $\Phi_e$ for the cylinder.

• There are no other charges that contribute appreciably to the flux calculation.
• The cylinder is aligned with respect to the line so that its bases are perpendicular to the line, and its wall is parallel (as described).

• We represent the electric flux through a surface with:

$$\Phi_e=\int\vec{E}\bullet \text{d}\vec{A}$$

• We represent the electric field due to a line of uniform surface charge density with:

$$\vec{E} = \frac{\lambda}{2\pi r\epsilon_0}\hat{r}$$

• We represent the situation with the following diagram.

First, we evaluate the situation qualitatively. Consider the electric field lines of the charged line: 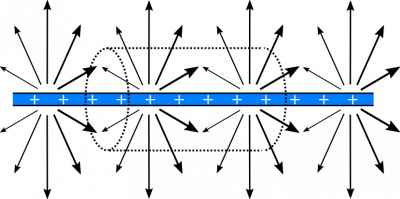It's a little tough to demonstrate the field lines with only two dimensions to draw on, but you can imagine that the thicker arrows point out of the page more, and the thinner arrows point into the page more. In essence, each arrow should point directly away from and perpendicular to the line of charge, as indicated in the formula for electric field from a line charge.

The electric field is parallel to the bases of the cylinder, so there are no electric field lines entering or exiting from the bases. So the flux through the bases should be $0$. For the wall of the cylinder, the electric field lines are perpendicular to the surface, which means they are parallel to the area-vectors. These facts will greatly simplify our integral calculation of the flux.

$$\begin{align*} \Phi_{\text{total}} &= \Phi_{\text{bases}}+\Phi_{\text{wall}} \\ &= 0 + \int_{\text{wall}}\vec{E}\bullet \text{d}\vec{A} \\ &= \int_{\text{wall}}E\hat{r}\bullet \text{d}A\hat{r} \\ &= E\int_{\text{wall}}\text{d}A \\ &= EA_{\text{wall}} \\ &= \frac{\lambda}{2\pi R \epsilon_0}\cdot 2\pi R l \\ &= \frac{\lambda l}{\epsilon_0} \end{align*}$$ When we plug in values for $\lambda$, $l$, and $\epsilon_0$, we get $\Phi_{\text{cube}}=5.08\cdot 10^6\text{ Vm}$.

Notice that in the next section of notes, we define “Gauss' Law”, which states that the total flux through a close surface is the amount of charge enclosed divided by $\epsilon_0$. A quick check for this example shows us that the charge enclosed by the cylinder covers a length of $l$, which means the charge is $\lambda l$. If we had used Gauss' Law, we would have quickly found that

$$\Phi_{\text{cylinder}}=\frac{Q_{\text{enclosed}}}{\epsilon_0}=\frac{\lambda l}{\epsilon_0}$$ This is the same result! An alternative question for this example could have been: What is the electric field due to a uniformly charged line? If we were not given the electric field at the beginning, we could have used symmetry arguments and Gauss' Law to work backwards, starting with the charge enclosed, and then using the integral formula for electric flux to solve for the electric field. There are sometimes electric fields that we do not know off-hand, and Gauss' Law is often the best tool to find them.