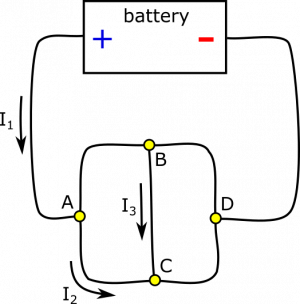
Suppose you have the circuit below. Nodes are labeled for simplicity of discussion. you are given a few values: $I_1=8 \text{ A}$, $I_2=3 \text{ A}$, and $I_3=4 \text{ A}$. Determine all other currents in the circuit, using the Current Node Rule. Draw the direction of the current as well.

• $I_1=8 \text{ A}$, $I_2=3 \text{ A}$, and $I_3=4 \text{ A}$.
• $I_1$, $I_2$, and $I_3$ are directed as pictured.

• All other currents (including their directions).

• The current is not changing.
• All current in the circuit arises from other currents in the circuit.

• We represent the situation with diagram given.
• We represent the Node Rule as $I_{in}=I_{out}$.

Let's start with node $A$. Incoming current is $I_1$, and outgoing current is $I_2$. How do we decide if $I_{A\rightarrow B}$ is incoming or outgoing? We need to bring it back to the Node Rule: $I_{in}=I_{out}$. Since $I_1=8 \text{ A}$ and $I_2=3 \text{ A}$, we need $I_{A\rightarrow B}$ to be outgoing to balance. To satisfy the Node Rule, we set $$I_{A\rightarrow B} = I_{out}-I_2 = I_{in}-I_2 = I_1-I_2 = 5 \text{ A}$.