Find the capacitance of a cylindrical capacitor. The structure of the capacitor is a cylindrical shell inside another cylindrical shell. The two shells become oppositely charged when the capacitor is connected to a power source. The length of the cylinders is $L$, and their radii are $a$ and $b$, with $a<b$.

• The length is $L$
• The inner radius is $a$, and the outer radius is $b$.
• The two cylinders are shells, so all charge will accumulate on the surface.

• Capacitance

• The cylinders are much longer than they are far from one another, i.e., $L >> a, b$.

• We represent capacitance as $$C=\frac{Q}{\Delta V},$$ where $Q$ is the charge on one of the capacitor's conductors (cylinders, in this case), and $\Delta V$ is the potential difference between them.
• We represent the situation below.

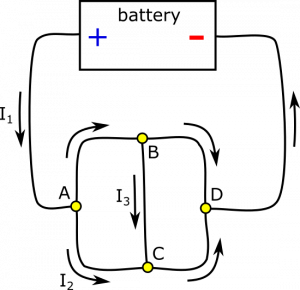
Let's start with node $A$. Incoming current is $I_1$, and outgoing current is $I_2$. How do we decide if $I_{A\rightarrow B}$ is incoming or outgoing? We need to bring it back to the Node Rule: $I_{in}=I_{out}$. Since $I_1=8 \text{ A}$ and $I_2=3 \text{ A}$, we need $I_{A\rightarrow B}$ to be outgoing to balance. To satisfy the Node Rule, we set $$I_{A\rightarrow B} = I_{out}-I_2 = I_{in}-I_2 = I_1-I_2 = 5 \text{ A}$$

We do a similar analysis for node $B$. Incoming current is $I_{A\rightarrow B}$, and outgoing current is $I_3$. Since $I_{A\rightarrow B}=5 \text{ A}$ and $I_3=4 \text{ A}$, we need $I_{B\rightarrow D}$ to be outgoing to balance. To satisfy the Node Rule, we set $$I_{B\rightarrow D} = I_{out}-I_3 = I_{in}-I_3 = I_{A\rightarrow B}-I_3 = 1 \text{ A}$$

For node $C$, incoming current is $I_2$ and $I_3$. There is no outgoing current defined yet! $I_{C\rightarrow D}$ must be outgoing to balance. To satisfy the Node Rule, we set $$I_{C\rightarrow D} = I_{out} = I_{in} = I_2+I_3 = 7 \text{ A}$$

Lastly, we look at node $D$. Incoming current is $I_{B\rightarrow D}$ and $I_{C\rightarrow D}$. Since there is no outgoing current defined yet, $I_{D\rightarrow battery}$ must be outgoing to balance. To satisfy the Node Rule, we set $$I_{D\rightarrow battery} = I_{out} = I_{in} = I_{B\rightarrow D}+I_{B\rightarrow D} = 8 \text{ A}$$

Notice that $I_{D\rightarrow battery}=I_1$. This will always be the case for currents going in and out of the battery (approximating a few things that are usually safe to approximate, such as a steady current). In fact, we could have treated the battery as another node in this example. Notice also that if you incorrectly reason about the direction of a current (incoming or outgoing), the calculation will give a negative number for the current. The Node Rule is self-correcting. A final diagram with directions is shown below.