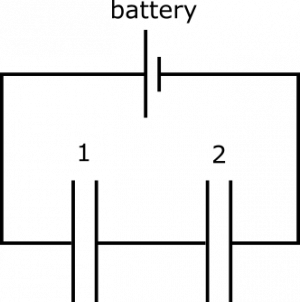
Suppose you have the following circuit. Capacitors are labeled 1 and 2 for convenience of reference. You know that the circuit contains a 12-Volt battery, $Q_1=4.5 \mu\text{C}$, and $C_2=0.5 \mu\text{F}$. What is the capacitance of Capacitor 1? What happens to the charge on the capacitors if we insert a dielectric material with dielectric constant $\epsilon = 3\epsilon_0$ into Capacitor 1?

• $\Delta V_{\text{bat}} = 12\text{ V}$
• $Q_1 = 4.5 \mu\text{C}$
• $C_2 = 0.5 \mu\text{F}$
• $\epsilon = 3\epsilon_0$

• $C_1$
• How the charges change when the dielectric is inserted.

• The wire has very very small resistance when compared to the other resistors in the circuit.
• We are measuring things like potential differences and charges when the circuit is in a steady state.
• Approximating the battery as a mechanical battery.

• We represent capacitance as $$C=\frac{Q}{\Delta V}$$
• We represent the equivalent capacitance of multiple capacitors arranged in series as

$$\frac{1}{C_{\text{equiv}}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+\ldots$$

• We represent the situation with diagram given above.

Shortly, we will constrain our calculations to just Resistors 1 and 2. We don't have any information on Resistor 2, so our approach will be to find the equivalent resistance of 1 and 2, and then focus on just Resistor 2 using equation (3). The first steps in our approach will be to find the current and potential difference across these two resistors. Note, this is not the only approach that would work! Another way would be to find individual potential difference across each resistor, and then focusing on Resistor 2 from there. See if you can think of yet another method…

We can use the Loop Rule – equation (4) – to find the potential difference across these two resistors. The potential difference across the battery has opposite sign as the differences across the resistors, if we consider the circuit as a loop of individual differences. We write:

$$\Delta V_{bat} = \Delta V_1 + \Delta V_2 + \Delta V_3$$ Since we know $\Delta V_{bat}$ and $\Delta V_3$, we can plug in and solve: $\Delta V_1 + \Delta V_2 = 6 \text{ V}$.

We can find current through the circuit using equations (1) and (2). We can write the power dissipated through Resistor 1 as

$$P_1={I_1}^2R_1$$ Since we know $P_1$ and $R_1$, we can plug in and solve for $I_1=\sqrt{P_1/R_1}=0.1 \text{ A}$. Recall that the Node Rule tells us that the current is the same everywhere in the circuit, since the entire circuit is arranged in a series. so $I=I_1=0.1 \text{ A}$.

We now have enough information to find the equivalent resistance of the two resistors, using Ohm's Law – equation (1). We write:

$$R_{\text{1 and 2, equivalent}}=\frac{\Delta V_1 + \Delta V_2}{I}=60 \Omega$$ Now, equation (3) tells us $R_{eq}=R_1+R_2$, so $$R_2=R_{eq}-R_1 = 50\Omega$$ The power dissipated across Resistor 2 can be found using the same rewriting of equation (2) as above: $$P_2=I^2R_2= 0.6 \text{ W}$$