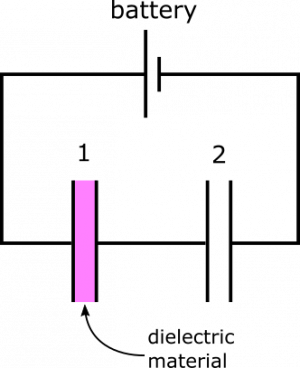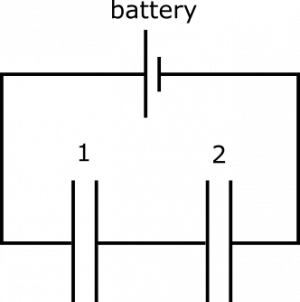
Suppose you have the following circuit. Capacitors are labeled 1 and 2 for convenience of reference. You know that the circuit contains a 12-Volt battery, $Q_1=4.5 \mu\text{C}$, and $C_2=0.5 \mu\text{F}$. What is the capacitance of Capacitor 1? What happens to the charge on the capacitors if we insert a dielectric material with dielectric constant $k = 3$ into Capacitor 1?

• $\Delta V_{\text{bat}} = 12\text{ V}$
• $Q_1 = 4.5 \mu\text{C}$
• $C_2 = 0.5 \mu\text{F}$
• $k = 3$

• $C_1$
• How the charges change when the dielectric is inserted.

• The wire has very very small resistance when compared to the other resistors in the circuit.
• We are measuring things like potential differences and charges when the circuit is in a steady state.
• Approximating the battery as a mechanical battery.

• We represent capacitance as $$C=\frac{Q}{\Delta V}$$
• We represent the equivalent capacitance of multiple capacitors arranged in series as

$$\frac{1}{C_{\text{equiv}}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+\ldots$$

• We represent the situation with diagram given above.

Let's find $C_1$. In order to use the equation for equivalent capacitance of capacitors in series, as we have here, we first need the equivalent capacitance of the entire circuit. Remember that the charge on the capacitors in series should be the same, so $Q_{\text{equiv}}=Q_1=Q_2$. Now, we can write:

$$C_{\text{equiv}}=\frac{Q_{\text{equiv}}}{\Delta V_{\text{bat}}}=0.375 \mu\text{F}$$

Now we can solve for C_2 using

$$\frac{1}{C_{\text{equiv}}}=\frac{1}{C_1}+\frac{1}{C_2}$$ This gives us $C_1 = 0.5 \mu\text{F}$

Now we need to consider what happens when we insert a dielectric. It might look something like the circuit above. A description of what a dielectric does in a capacitor is here. Its effect on capacitance is:

$$C =\frac{k\epsilon_0 A}{d}$$

So when we insert the dielectric, we have a new capacitance for Capacitor 1: $C_{\text{1, new}}=kC_1=4.5 \mu\text{F}$. To find the new value that the capacitors are charged to, we return to the equivalent capacitance of the circuit:

$$\frac{1}{C_{\text{equiv, new}}}=\frac{1}{C_{\text{1, new}}}+\frac{1}{C_2}$$ This yields $C_{\text{equiv, new}}=0.45 \mu\text{F}$. Now, we can find the new charge: $$Q_{\text{new}} = C_{\text{equiv, new}}\Delta V_{\text{bat}} = 5.4 \mu\text{C}$$