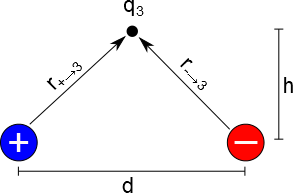
If you have more than two point charges, you can still use the same process to find the electric force. Suppose you have a third positive charge in between the positive and negative charges of the dipole as shown. What would be the force on this third charge?

We start by finding the net electric field at the location of $q_3$ using superposition, which is given by the electric field from the positive charge and the electric field from the negative charge. $$\vec{E}_{net}=\vec{E}_{+}+\vec{E}_{-}$$

The electric field from the positive charge is given by: $$E_{+}=\frac{1}{4\pi\epsilon_0}\frac{q_{+}}{(r_{+ \rightarrow 3})^3}\vec{r}_{+ \rightarrow 3}$$ where $\vec{r}_{+ \rightarrow 3}= \langle d/2, h,0 \rangle$ because it points from the positive charge to the location of $q_3$. $r_{+ \rightarrow 3}$ is the magnitude of $\vec{r}_{+ \rightarrow 3}$ so $$r_{+ \rightarrow 3}=\sqrt{(d/2)^2+h^2}$$

So this means that $\vec{E}_{+}$ is given by: $$E_{+}=\frac{1}{4\pi\epsilon_0}\frac{q_{+}}{(\sqrt{(d/2)^2+h^2})^3}\langle d/2, h,0 \rangle$$

Similarly, we can find the electric field from the negative charge: $$E_{-}=\frac{1}{4\pi\epsilon_0}\frac{q_{-}}{(r_{- \rightarrow 3})^3}\vec{r}_{- \rightarrow 3}$$ where $\vec{r}_{- \rightarrow 3}= \langle -d/2, h,0 \rangle$ because it points from the negative charge to the location of $q_3$. $r_{- \rightarrow 3}$ is the magnitude of $\vec{r}_{- \rightarrow 3}$ so $$r_{- \rightarrow 3}=\sqrt{(-d/2)^2+h^2}=\sqrt{(d/2)^2+h^2}$$

So this means that $\vec{E}_{-}$ is given by: $$E_{-}=\frac{1}{4\pi\epsilon_0}\frac{q_{-}}{(\sqrt{(d/2)^2+h^2})^3}\langle -d/2, h,0 \rangle$$

So the net electric field is given by: $$\vec{E}_{net}=\frac{1}{4\pi\epsilon_0}\frac{q_{+}}{(\sqrt{(d/2)^2+h^2})^3}\langle d/2, h,0 \rangle + \frac{1}{4\pi\epsilon_0}\frac{q_{-}}{(\sqrt{(d/2)^2+h^2})^3}\langle -d/2, h,0 \rangle$$

If we assume the dipole charges are equal in magnitude (but still opposite in sign) then this becomes: $$\vec{E}_{net}=+\frac{1}{4\pi\epsilon_0}\frac{q}{(\sqrt{(d/2)^2+h^2})^3}\langle d/2, h,0 \rangle - \frac{1}{4\pi\epsilon_0}\frac{q}{(\sqrt{(d/2)^2+h^2})^3}\langle -d/2, h,0 \rangle$$

$$\vec{E}_{net}=\frac{1}{4\pi\epsilon_0}\frac{q}{(\sqrt{(d/2)^2+h^2})^3}(\langle d/2, h,0 \rangle - \langle -d/2, h,0 \rangle)$$

$$\vec{E}_{net}=\frac{1}{4\pi\epsilon_0}\frac{q}{(\sqrt{(d/2)^2+h^2})^3}\langle (d/2+d/2), (h-h),0 \rangle$$

$$\vec{E}_{net}=\frac{1}{4\pi\epsilon_0}\frac{q}{(\sqrt{(d/2)^2+h^2})^3}\langle d, 0,0 \rangle$$

So this is the net electric field at $q_3$ from both the positive and negative dipole charges. Finally to find the force on $q_3$, we use: $$\vec{F}_{q_3}=q_3\vec{E}_{net}=\frac{1}{4\pi\epsilon_0}\frac{q_3*q}{(\sqrt{(d/2)^2+h^2})^3}\langle d, 0,0 \rangle$$

This force only points in the $\hat{x}$ direction, which makes sense. Because $q_3$ is positive, we know that it should be repelled from the positive charge and attracted toward the negative charge. As much as the positive charge wants to push it away, the negative charge wants to pull it back so there is no change in the $\hat{y}$ direction, but both charges want to send $q_3$ to the right.

Since dipoles occur frequently in nature (we can model any atom as dipole), it is often useful to have simplified equation for the electric field of a dipole. If we start with the equation that we found for the electric field of the dipole above:

$$\vec{E}_{net}=\frac{1}{4\pi\epsilon_0}\frac{q}{(\sqrt{(d/2)^2+h^2})^3}\langle d, 0,0 \rangle$$

Now if we assume that we are really far away from the dipole, then this would mean that $h$ is much much larger than the separation of $d$. This allows us to simplify the denominator. If $h>>d$, then the $h^2$ of $(d/2)^2+h^2$ will be significantly larger than the $(d/2)^2$ term. So we can approximate: $$(d/2)^2+h^2 \approx h^2$$ Using this with our electric field equation gives: $$\vec{E}_{net} \approx \frac{1}{4\pi\epsilon_0}\frac{q}{(\sqrt{(h^2})^3}\langle d, 0,0 \rangle$$ $$\vec{E}_{net} \approx \frac{1}{4\pi\epsilon_0}\frac{q}{h^3}\langle d, 0,0 \rangle$$ Note, this electric field equation is only true for points far away from the dipole and perpendicular to the dipole axis.

We could also follow a similar process to find the electric field for points far away but on the same axis as the dipole. This would consist of finding the electric field from both the positive and negative charge, adding those fields together through superposition, and making an approximation that the separation between the charges is much smaller than the distance to the point of interest. This will give you an approximate electric field on the axis of: $$|\vec{E}_{axis}|=\frac{1}{4\pi\epsilon_0}\frac{2qd}{r^3}$$ where r is the distance from the middle of the dipole to the point of interest, d is separation between the positive and negative charges, and q is the magnitude of one of the charges.

Note this is only the magnitude of the electric field. The direction depends on which side of the dipole you are considering. (If you are closer to the negative charge, the electric field will point toward the negative charge. If you are closer to the positive charge, the electric field will point away from the positive charge.)