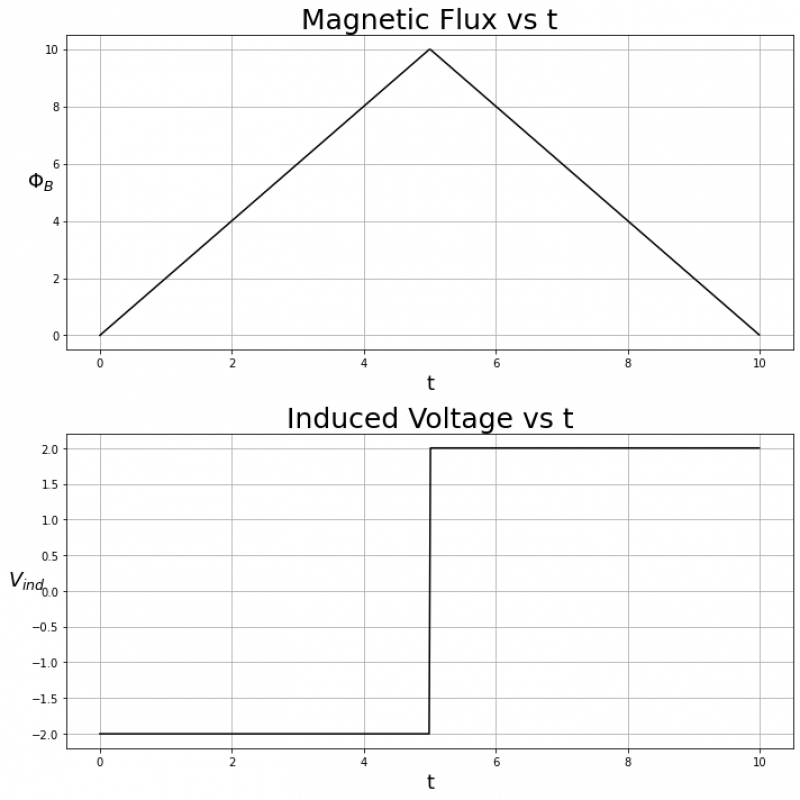
In these notes, we will examine a few examples of changing magnetic fluxes and associated induced voltages. First let's consider when $\Phi_B$ rises and falls linearly with the same magnitude of slope:

From $t = 0$ to $t = 5$, $\Phi_B(t)$ has a constant positive slope, so $V_{ind}$ will be constant and negative. Conversely, from $t = 5$ to $t = 10$, $\Phi_B(t)$ has a constant negative slope, so $V_{ind}$ will be constant and positive.

Specifically, in this case $\Phi_B(t)$ is defined as: $$\Phi_B(t)= \begin{cases} 2t & \text{if } 0<t<5\\ -2t & \text{if } 5<t<10 \end{cases}$$ Which means $\frac{d \Phi_B}{dt}$ is: $$\frac{d \Phi_B}{dt}= \begin{cases} 2 & \text{if } 0<t<5\\ -2 & \text{if } 5<t<10 \end{cases}$$ Which finally means that $V_{ind}$ is: $$V_{ind}= \begin{cases} -2 & \text{if } 0<t<5\\ 2 & \text{if } 5<t<10 \end{cases}$$

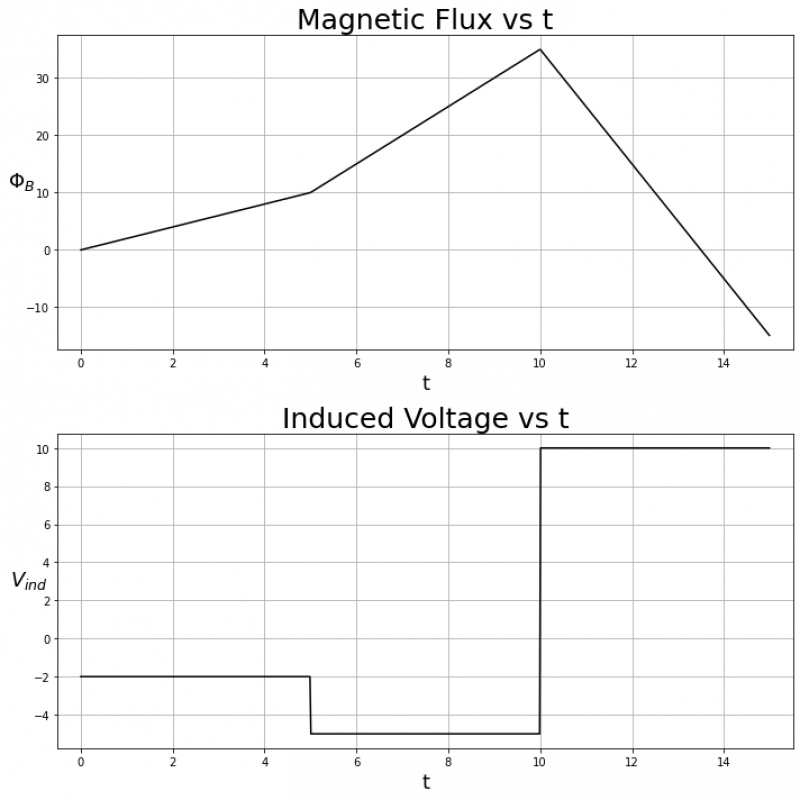
Next, let's consider an example with a few different slopes:

We can see that from $t=0$ to $t = 10$, $\Phi_B(t)$ has a positive slope, so $V_{ind}$ is negative on that time interval. However, $\Phi_B(t)$ is steeper from $t=5$ to $t=10$, so $V_{ind}$ is more negative on that time interval than from $t = 0$ to $t = 5$. From $t = 10$ to $t = 15$, $\Phi_B(t)$ has a constant and negative slope, so $V_{ind}$ is constant and positive on that time interval.

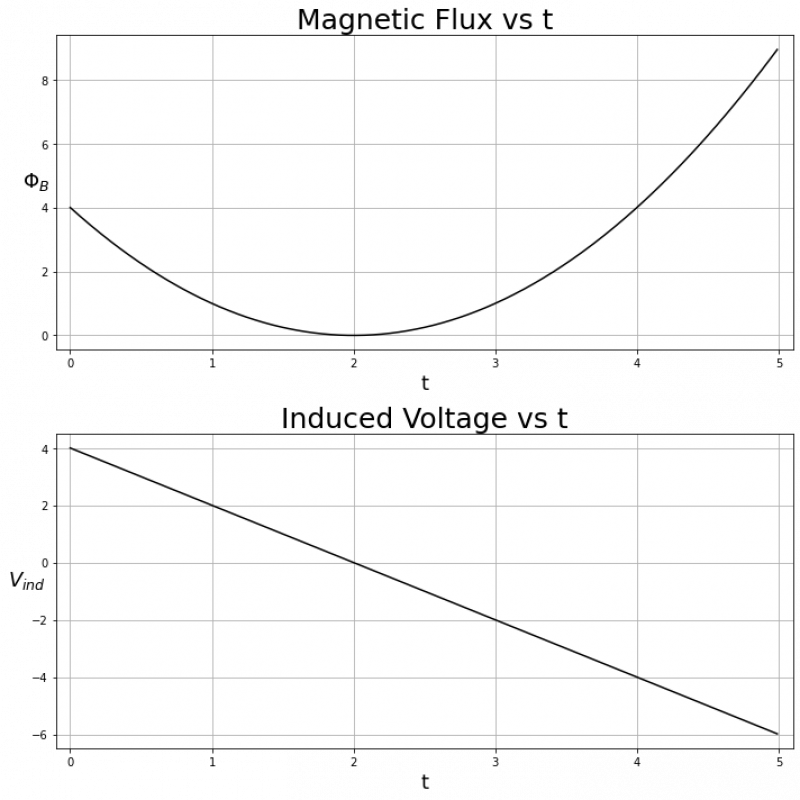
Finally, let's look at an example with a non-linear $\Phi_B(t)$:

$\Phi_B(t)$ looks like a quadratic centered about t = 2. We can see that while $\Phi_B(t)$ is decreasing ($0<t<2$), $V_{ind} is positive, and while$\Phi_B(t)$is increasing ($2<t<8$),$V_{ind} is negative.