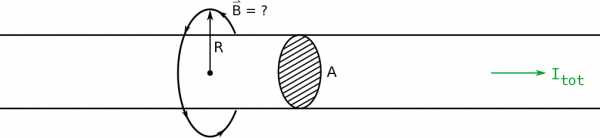
Now, that we have built the two sides of Ampere's law, let's review the steps and put everything together to find the magnetic field outside of a long straight wire. This model of a long straight wire is usually pretty good for many situations where you want to determine the magnetic field near the wire. When you start to get farther away from the wire, the ends of the wire become problematic since the magnetic field is no longer perfectly circular. (In this case, the Biot-Savart model would be much better.)

The last step here is to piece together the left and right sides of Ampere's law to find the magnetic field outside of a long straight wire. As a reminder, the original equation was:

$$\oint \vec{B} \bullet d\vec{l} = \mu_0 I_{enc}$$

Amperian loop of radius, $R$, around a wire with current, $I$

For the left hand side, we argued the magnetic field curls around the wire. So long as the wire has a uniform steady current, that magnitude of that magnetic field will be constant at any fixed distance from the wire. This lead us to derive the left-hand side of Ampere's Law for an Amperian loop of radius $R$ centered on the wire,

$$\oint \vec{B} \bullet d\vec{l} = B \oint dl = B 2\pi R$$

where we said that $R$ is greater than the radius of the wire.

For the right hand side then, our Amperian loop is larger than the radius of the wire, so the total enclosed current is just $I_{tot}$. This leaves the left hand side of Ampere's Law to simply be,

$$\mu_0 I_{enc} = \mu_0 I_{tot}.$$

Combining the two sides of Ampere's law, we can find the magnitude of the magnetic field produced by the wire at a distance $R$ from the center of the wire.

$$\oint \vec{B} \bullet d\vec{l} = \mu_0 I_{enc}$$ $$B \oint dl = \mu_0 I_{tot}$$ $$B 2\pi R = \mu_0 I_{tot}$$ $$ B =\mu_0\dfrac{I_{tot}}{2\pi R}$$

This is exactly the result we obtained with Biot-Savart for a very long wire (but we had to do a much more complicated integral).

The final step here is to ask what is the direction of this B-field? With Ampere's Law, our magnetic field vector turned into a magnitude when we simplified the dot product. Therefore, to find the direction of the field you must use the right-hand rule after (or before) you calculate the magnitude using Ampere's Law. When you do this, you will find that the magnetic field still curls around the current wire in the same way.

There are a few cases (besides outside a long wire) where Ampere's law is useful, including inside wires (as we mentioned before), solenoids, and toroids. In these other cases, the details may be different, but the steps that you would take would still be the same. These would include:

1. Figure out and draw the general shape of the magnetic field.
2. Choose an Amperian loop that a) goes through your observation point, b) follows the magnetic field (to simplify the dot product) and c) has a constant magnetic field along the length of the loop (to pull the B out of the integral). This lets you simplify the left side of the integral.
3. Find the current enclosed by the loop (maybe using current density if you need a fraction of the total current).
4. Solve for the magnitude of the magnetic field
5. Double check the direction of the magnetic field using the right hand rule.