This is an old revision of the document!
Section 21.3 from Matter and Interaction (4th edition)
Electric Flux through Curved Surfaces
We talked already about how to calculate the electric flux through a flat surface and through an enclosed cube for a constant electric field. But what happens if the field is not constant? Or what if the surface is no longer flat? These notes will show how we modify the electric flux equation to account for varying fields and curved surfaces.
Curved Surfaces
Area Vectors
Before we said that for a flat surface, the area vector is given by the magnitude of the area times the vector that points perpendicular to the area. This makes sense for a flat surface, where the area vector will point in the same direction for all points on the surface. However, for a curved surface, this no longer makes sense. It becomes impossible to use a single vector to describe the surface.
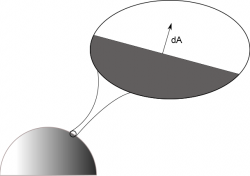
But if we zoom in on a very small piece of the area (call this dA), this extremely small area will appear to be flat. Thus, we can write the area vector for this very small piece of area using our normal rule. Namely, that the vector for the very small piece of area ($d\vec{A}$) will be equal to the magnitude of the small chunk of area ($dA$) times the vector that is perpendicular to that small chunk ($\hat{n}$): $$d\vec{A}=dA \hat{n}$$
For example, take a hemisphere shell as a surface area. On the very top of the hemisphere, the little piece of area is horizontally flat, so the $d\vec{A}$ at this location would point straight up. If you move to either side of the top of the hemisphere, the dA would be locally flat (tangent to the hemisphere surface), so at that location, the $d\vec{A}$ would point perpendicular to the surface. No matter where you pick as your dA, the $d\vec{A}$ should point perpendicular to that small piece of area. In the case of the curved part of a hemisphere (or a whole sphere for that matter), the $d\vec{A}$'s all point radially away from the center of the sphere. So we could write any general $d\vec{A}$ for a sphere as: $$d\vec{A}=dA \hat{r}$$
Electric Flux
To find the electric flux then, we must add up the electric flux through each little bit of area on the surface. In terms of calculus, this would mean we first would write the little bit of flux ($d\Phi_e$) as the cross product of the electric field through the little bit of area ($\vec{E}$) and the little area vector ($d\vec{A}$): $$d\Phi_e = \vec{E} \bullet d\vec{A}$$ Then to add up all of the little bits of electric flux, we would take the integral of both sides (over the whole area that you have): $$\Phi_e=\int d\Phi_e=\int \vec{E} \bullet d\vec{A}$$ This equation for electric flux is the most general equation that is always true - we have not made any assumptions about the kind of electric field or area shape. This means that this equation will always work to calculate the electric flux; however, the calculus can become very complicated very quickly if you are not careful. The next section of notes will explain how we make use of symmetry to make these calculations easier.
Making Use of Symmetry
When we look at this equation for flux, there are two places where symmetry can make our calculations much easier. First, we want to simplify the dot product - either by picking surfaces with $d\vec{A}$'s that are perpendicular to the electric field (giving zero flux) or by picking surfaces with $d\vec{A}$'s that are parallel to the electric field. If everywhere along the surface the $d\vec{A}$ is parallel to the electric field, then the dot product turns into a normal multiplication of the vector magnitudes: $$\Phi_e= \int \vec{E} \bullet d\vec{A} = \int EdA$$ Note you can only make this simplification if $\vec{E}$ is always parallel to $d\vec{A}$ on the surface. The second place we can use symmetry to help simplify the integral is when the electric field is constant everywhere along the area surface. If this is true, then E is a constant with respect to dA, so we can pull it out of the integral: $$\Phi_e = \int EdA=E \int dA$$ Then the integral of dA is simply A, so we get: $$\Phi_e = EA$$ where E is the magnitude of the electric field at the surface and A is the total surface area. This is an amazingly simple answer for a curved surface, so we will be looking particularly at surfaces and charges that have:
- parallel $d\vec{A}$'s to the electric field
- constant electric fields along the surface.
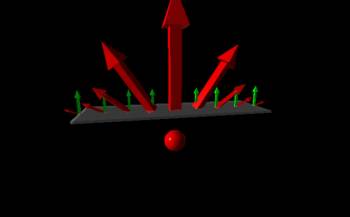
As an example, let's look at the electric field from a positive point charge, which points radially away from the point charge (shown by the red arrows). If we imagine a rectangular plane above the point charge, then the electric field vectors that would point through that plane would both change direction and change in magnitude all over the surface. Since the electric field vectors have different directions all over the plane but the dA vectors all point up for the plane (shown by the green arrows), this means we cannot easily simplify the dot product in the electric flux equation. On top of that, the electric field is not constant along the plane since the magnitudes of the vectors change. In this case, the integral to find the flux would be extremely difficult and would need to account for the changing angle of the vectors and the changing size of the field (aka we do not want to do that).
Instead, imagine a spherical shell or bubble around the point charge. In this case, the $d\vec{A}$'s would point radially outward from the bubble at every point along the surface (again shown by the green vectors). Likewise, for every dA, the electric field points radially away from the point charge (shown by red arrows). This means that the $d\vec{A}$ is always perpendicular to $\vec{E}$ for a given location, so we can simplify the dot product to a simple multiplication. $$\Phi_e= \int \vec{E} \bullet d\vec{A} = \int EdA$$ Also, since the bubble has a set radius, everywhere along the surface has the same magnitude of the electric field. This means that E is constant along the surface (with respect to the surface area) so we can pull the E out of the integral. Then integrating dA over the whole surface, simply gives the surface area. $$\Phi_e = \int EdA=E \int dA = EA$$ In this case, E would be the magnitude of the electric field from a point charge at the radius of the shell. If we say that the radius of the shell is some distance c, then $r = c$. So we can write the electric from the point charge as: $$E = \frac{1}{4\pi\epsilon_0}\frac{q}{c^2}$$ and A would be the surface area of a sphere with a radius of $r=c$. $$A= 4\pi c^2$$ Putting those together we find the electric flux through the sphere to be: $$\Phi_e = EA =\frac{1}{4\pi\epsilon_0}\frac{q}{c^2}4\pi c^2$$ $$\Phi_e = \frac{q}{\epsilon_0}$$ (This equation then says that the electric flux through the spherical shell is equal to the charge inside the spherical bubble divided by a constant, which is Gauss's Law.)
Thus, we want to pick surfaces that have high amounts of symmetry with our charge distributions because this will make our calculations of electric flux much more doable.