Suppose we have a ring with radius $R$ that has a uniform charge distribution with total charge $Q$. What is the electric field at a point $P$, which is a distance $z$ from the center of the ring, along a line perpendicular to the plane of the ring? What happens to the electric field as $z = 0$ (i.e., when $P$ is in the center of the ring rather than above it)? Why?

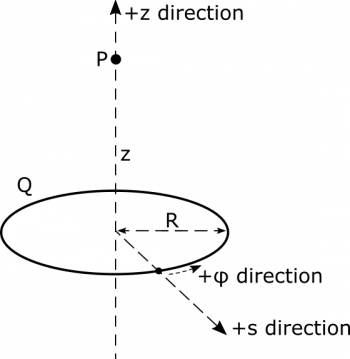
• The point $P$ is a distance $z$ away from the center of the ring.
• The ring has a charge $Q$, which is uniformly distributed.

• Electric field at $P$.
• $\text{d}Q$ and $\vec{r}$

• The electric field at $P$ is due solely to the ring.
• The thickness of the ring is infinitesimally small, and we can approximate it as a circle.
• The ring is not discharging – $Q$ is constant.

• The electric field from the point charge can be written as $$\vec{E} = \frac{1}{4\pi\epsilon_0}\frac{q}{r^3}\vec{r}$$
• We can represent the ring and $P$ as follows, with coordinates chosen conveniently. We choose cylindrical coordinates because we will be integrating over the length of the ring, and being able to represent its radius as constant will simplify calculations.

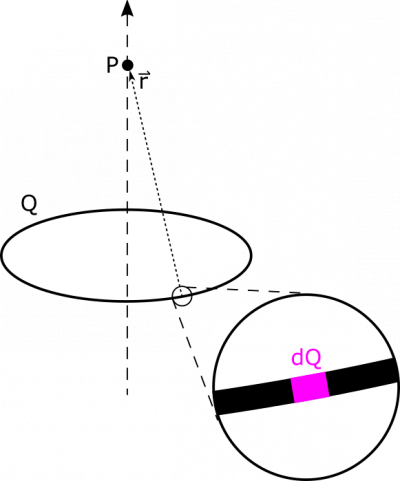
• We can represent $\text{d}Q$ and $\vec{r}$ for our ring as follows:

Just like before, we want to write our $\text{d}Q$ in terms of the little bit of length; however this time, our $\text{d}Q$ is spread over a little bit of the ring. We could try to write this little bit of length in terms of $\text{d}x$ or $\text{d}y$, but that gets complicated because we need the length to represent a little piece of the ring. Instead, we will think of this little piece of the ring in terms of the little bit of the angle it represents (this length of a circle is sometimes referred to as arc length).

So the $\text{d}Q$ in our representation takes up a small angle out of the whole circle, which we can call $\text{d}\phi$. The length of our $\text{d}Q$ is therefore $R\text{d}\phi$ (which comes from the arc length formula). Remember from the notes on line charges that we can write $\text{d}Q=\lambda\text{d}l$. Since the charge $Q$ is uniformly distributed on the ring, we use the length of the ring or circumference ($2\pi R$) to write the line charge density $\lambda=Q/2\pi R$. Now, we have an expression for $\text{d}Q$: $$\text{d}Q=\lambda\text{d}l=\frac{Q}{2\pi R}R\text{d}\phi=\frac{Q\text{d}\phi}{2\pi}$$

To find an expression for $\vec{r}$, we can also consult the representation. $\vec{r}$ points from the location of $\text{d}Q$ to the point $P$. The location of $\text{d}Q$ is $\vec{r}_{\text{d}Q}=R\hat{s}$. This unit vector $\hat{s}$ may be unfamiliar, since we are used to working in Cartesian coordinates. $\hat{s}$ is the unit vector that points along the radius of a cylinder centered on the $z$-axis in our cylindrical coordinate system. In fact, $\hat{s}$ actually depends on $\phi$, and is more appropriately written as a function in terms of $\phi$, or $\hat{s}(\phi)$. We do not acknowledge the $\phi$-dependence in our solution here, because as you will soon see, all terms containing $\hat{s}$ will disappear.

The location of $P$ is $\vec{r}_P=z\hat{z}$. Then we have $\vec{r}=\vec{r}_P-\vec{r}_{\text{d}Q}=z\hat{z}-R\hat{s}$. This makes sense looking at the direction $\vec{r}$ points in our representation – it points in towards the center ($-\hat{s}$ bit) and points up toward P ($+\hat{z}$ bit). We also need to know the magnitude $|\vec{r}|$, which is simply $\sqrt{\vec{r}\bullet\vec{r}}=\sqrt{R^2+z^2}$.

The electric field $\text{d}\vec{E}$ from our charge $\text{d}Q$ is then $$\text{d}\vec{E}=\frac{1}{4\pi\epsilon_0}\frac{\text{d}Q}{r^3}\vec{r}=\frac{1}{8\pi^2\epsilon_0}\frac{Q\text{d}\phi}{(R^2+z^2)^{3/2}}(z\hat{z}-R\hat{s})$$

From here, we can set up the integral for calculating the electric field: $$\vec{E}=\int\text{d}\vec{E}=\int\frac{1}{8\pi^2\epsilon_0}\frac{Q\text{d}\phi}{(R^2+z^2)^{3/2}}(z\hat{z}-R\hat{s})$$

There are still a couple issues to sort out before we proceed. First, what are the limits of integration? We are integrating over $\text{d}\phi$, which represents a small slice of the ring, as shown in our representation. We want to integrate over all of the slices of the ring, so we set our limits of integration to cover all of the angles in the circle: $0$ to $2\pi$ (which are the starting and ending values for $\phi$).

The second issue has to do with the $\hat{s}$ terms, since $\hat{s}$ depends on $\phi$. Before we proceed, let's split up the integral for clarity: $$\vec{E}=\frac{Q}{8\pi^2\epsilon_0}\int_0^{2\pi}\frac{\text{d}\phi}{(R^2+z^2)^{3/2}}(z\hat{z}-R\hat{s})=\frac{Q}{8\pi^2\epsilon_0}\left(\int_0^{2\pi}\frac{z\text{d}\phi}{(R^2+z^2)^{3/2}}\hat{z}-\int_0^{2\pi}\frac{R\text{d}\phi}{(R^2+z^2)^{3/2}}\hat{s}\right)$$

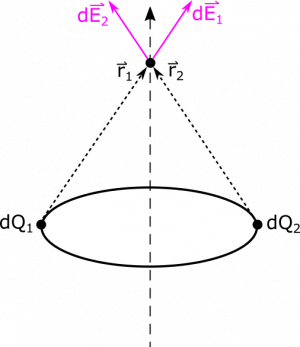
Since $\hat{s}$ depends on $\phi$, $\hat{s}$ is not constant over the path of our integration. We can actually use the symmetry of the example to get rid of this issue: Notice that the ring and the point $P$ do not change when we rotate them about $z$-axis. We call this “rotational symmetry about the $z$-axis”. From this, we can argue that the electric field vector at $P$ must also not change when we rotate it about $z$-axis, meaning that it has no radial component! All the $\hat{s}$ components in our electric field vector calculation must cancel out. This makes sense, as opposite points in the ring would have the same radial components, which will cancel out.

Now, we can write the electric field vector with limits on the integral, and leaving out the $\hat{r}$ components.

\begin{align*} \vec{E} &= \int_0^{2\pi}\frac{1}{8\pi^2\epsilon_0}\frac{Q\text{d}\phi}{(R^2+z^2)^{3/2}}z\hat{z} \\ &= \frac{1}{8\pi^2\epsilon_0}\frac{Qz\hat{z}}{(R^2+z^2)^{3/2}}\int_0^{2\pi}\text{d}\phi \\ &= \frac{1}{8\pi^2\epsilon_0}\frac{Qz\hat{z}}{(R^2+z^2)^{3/2}}2\pi \\ &= \frac{1}{4\pi\epsilon_0}\frac{Qz}{(R^2+z^2)^{3/2}}\hat{z} \end{align*}

As $z\rightarrow 0$, notice that $\vec{E}\rightarrow 0$, which makes sense when you consider the symmetry argument again. If $z=0$, then the point $P$ is at the center of the ring. Every electric field contribution from a given point on the ring will cancel out completely with the opposite point on the ring.