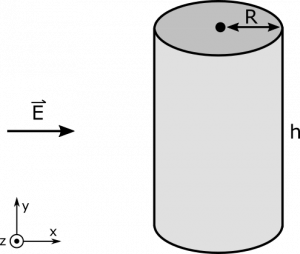
A constant electric field $\vec{E}$ is directed along the $x$-axis. A cylinder with radius $R$ and height $h$ is situated in the field so that the bases of the cylinder are parallel to the $xz$-plane. What is the electric flux through the cylinder?

• The cylinder is closed.
• The cylinder has radius $R$ and height $h$.
• The electric field is directed along the $x$-axis, which is parallel to the bases of the cylinder.

• $\Phi_e$
• $\vec{A}$ of cylinder, or $\text{d}\vec{A}$ pieces.

• The electric field is constant.
• The electric flux through the cylinder is due only to $\vec{E}$.
• We can approximate infinitesimally small pieces of the cylinder's area as flat.

• We represent the electric flux through a flat surface with:

$$\Phi=\vec{E}\bullet \vec{A}$$

• We represent the situation with the following diagram:

Before we dive into the math, let's reason about the nature of the situation. It will be helpful to visualize how the area vector $\text{d}\vec{A}$ would look for different parts of the cylinder's surface. Here is a visual from a couple perspectives, where each arrow represents the direction of $\text{d}\vec{A}$ at its location. 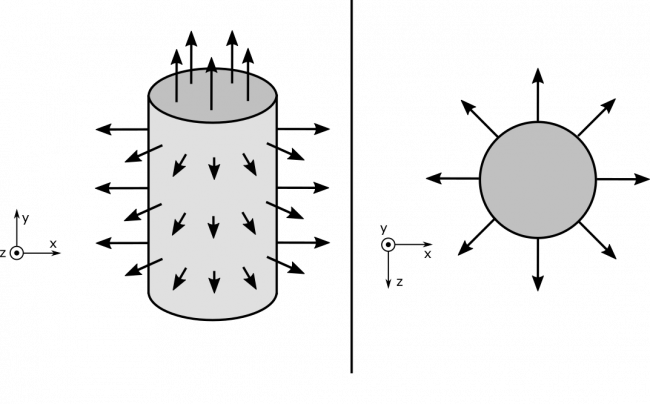Notice that the area vectors on the bases of the cylinder are pointing along the $y$-axis. Since the electric field is aligned with the $x$ axis, there will be no flux through the top and bottom of the cylinder. The math is right here: $$\Phi_{\text{top}}=\vec{E}\bullet\vec{A}_{\text{top}}=(E\hat{x})\bullet(\pi R^2\hat{y})=0$$ The same is true for bottom. For completeness, the math is here:

$$\Phi_{\text{bottom}}=\vec{E}\bullet\vec{A}_{\text{bottom}=(E\hat{x})\bullet(\pi R^2(-\hat{y}))=0$$