Now that we have the left bit of the equation, the next step is to talk about the right side of Ampere's law - namely the $\mu_0 I_{enc}$ bit. For an Amperian loop that outside of a single wire, this part is actually rather simple, but it starts to become more complicated when we consider loops inside the wire. As we said before, if the wire is a bit thick, we can investigate what happens to the magnetic field inside the wire as well outside. That's a tough job with the Biot-Savart law and is one of the places where Ampere's law can be super useful. On this page, we will focus on the right-hand side of Ampere's law, namely, the current through our Amperian loop.

The point of Ampere's Law is that it relates how curly the magnetic field is to how much current produces it.

$$\oint \vec{B}\cdot d \vec{l} = \mu_0 I_{enc}$$

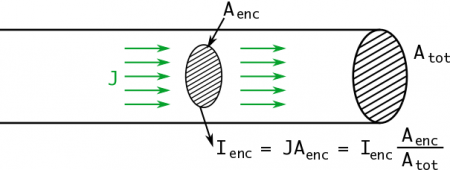
The right hand side describes the amount of current enclosed by the Amperian loop - that is, how much current runs through the inside of the loop. The figure below describes relationship between the loop and the enclosed current.

For the purposes of these notes, let's assume with have a thick wire with a total uniform current, $I_{tot}$.

If we are looking for the magnetic field outside of the wire, we will choose to draw the loop so that it's radius is bigger than the radius of wire. In this case, the total current that runs through the wire will pass through the Amperian loop, meaning the loop will enclose all the current. This is the simplest of cases where $I_{enc} = I_{tot}$.

When we want to find the magnetic field inside the wire, then we need pick the radius of the loop to be smaller than the radius of the wire. In this case, some of the current will pass through the loop but not all of the current. We need to be able to determine what fraction of the total current will pass through our loop.

To find $I_{encl}$, you will need to know the current density $J=I/A_{wire}$. For our purposes, we will assume a constant current density because we will deal with uniform currents. Hence the enclosed current is a fraction of the total,

$$I_{enc} = J A_{enc} = I_{tot} \dfrac{A_{enc}}{A_{tot}}$$

where both of these areas are cross-sectional areas. $A_{tot}$ is the total cross-sectional area of the wire and $A_{enc}$ is the cross-sectional area enclosed by the loop. This is very similar to how you found $Q_{encl}$ with Gauss's Law for Electric Fields.

As we discussed earlier, our canonical example with be the long straight wire. In this case, the wire is a bit thick, so that we can investigate what happens inside the wire as well. That's a tough job with the Biot-Savart law. We will use Ampere's law to find the magnetic field both inside and outside the thick wire. On this page, we will focus on the right-hand side of Ampere's law, namely, the current through our Amperian loop.

In this case, we will consider that the wire is a bit thicker than the average wire, so that it has a current density $J=I/A$. We will also assume that the current density is uniform in this class (upper-division courses may address non-uniform current densities). That is, at every point in the wire the same amount of charge per unit time per unit area exists. This will help us understand the power of Ampere's Law. The figure below shows a cross-section of the wire.