Circuit A: $$R_{eq}=R_1+R_2+R_3= 9 Ω$$ $$V_3>V_2>V_1$$ $$I_1=I_2=I_3$$

Circuit B: $$C_{eq}=(\frac{1}{C_1}+ \frac{1}{C_2}+ \frac{1}{C_3})^{-1}= 2.3 mF$$ $$Q_{1}=Q_{2}=Q_{3}$$ $$V_1>V_2>V_3$$

Circuit C: $$C_{eq}=C_1+C_2+C_3 = 21 mF$$ $$V_{1}=V_{2}=V_{3}$$ $$Q_3>Q_2>Q_1$$

Circuit D: $$R_{eq}=(\frac{1}{R_1}+ \frac{1}{R_2}+ \frac{1}{R_3})^{-1}= 0.92 Ω$$ $$V_{1}=V_{2}=V_{3}$$ $$I_1>I_2>I_3$$

Circuit A: $R_{eq}= 350 Ω$

Circuit B: $R_{eq}= 400 Ω$

Circuit C: $C_{eq}=235 μF$

Circuit D: $C_{eq}=176.25 μF$

Results:

Power Ranking: $P_1=P_2>P_1=P_3=P_4$

Results:

Power Ranking: $P_1>P_5>P_2>P_3>P_4$

Results:

Power Ranking: $P_5>P_3>P_1=P_2>P_4$

Results:

Power Ranking: $P_1>P_4>P_5>P_3>P_2$

Results:

Results:

Results:

Results:

Given:

$V_1= 9V$, $V_2= 6V$, $R=100 Ω$

Simplify Circuit:

• $R_1$ and $R_2$ in series, $R_1+R_2=200 Ω$

Node Rule:

• $I_1+I_2=I_3$

Loop Rule:

• Loop A: $V_1-I_1R_{12}-I_3R_3=0$
• Loop B: $I_3R_3-I_2R_4-V_2=0$
• Loop C: $V_1-I_1R_{12}-I_2R_4-V_2=0$

Solution:

$I_1=0.024A$, $I_2=0.018A$, $I_3=0.042A$

*note can use wolfram/online/calc to evaluate I from loop AND node rule equations

Given:

$V_1= 9V$, $V_2= 6V$, $R=100 Ω$

Simplify Circuit:

• $R_1$ || $R_2$, $R_{12}=50 Ω$

Node Rule:

• $I_1=I_2+I_3$

Loop Rule:

• Loop A: $V_1-I_1R_{12}-I_3R_3=0$
• Loop B: $ V_2 -I_2R_4 +I_3R_3=0$
• Loop C: $V_1-I_1R_{12-V_2}-I_2R_4=0$

Solution:

$I_1=0.12 A$, $I_2=0.09A$, $I_3=0.03A$

Given:

$V_1= 9V, V_2= 6V, R=100 Ω$

Simplify Circuit:

• $R_2$ and $R_3$ in series, $R_2+R_3=200 Ω$
• $R_4$ || $R_5$, $R_{12}=50 Ω$

Node Rule:

• $I_1=I_2+I_3$

Loop Rule:

• Loop A: $V_1-I_1R_1+V_2-I_1R_{45}=0$
• Loop B: $ -V_2-I_3R_{23}=0$
• Loop C: $V_1-I_1R_1-I_3R_{23}-I_1R_{45}=0$

Solution:

$I_1=0.06A$, $I_2=0.09A$, $I_3=-0.03A$

Given:

$V_1= 9V, V_2= 6V, R=100 Ω$

Simplify Circuit:

• $R_2$ and $R_3$ in series, $R_2+R_3=200 Ω$
• $R_1$||$R_{23}$, $R_{12}=66.667 Ω$

Node Rule:

• $I_1=I_2+I_3$

Loop Rule:

• Loop A: $V_1-I_1R_{123}- 0$
• Loop B: $ I_2R_{123}-V_2-I_3R_4=0$
• Loop C: $V_1-V_2-I_3R_4=0$

Solution:

$I_1=0.165A$, $I_2=0.135A$, $I_3=0.03A$

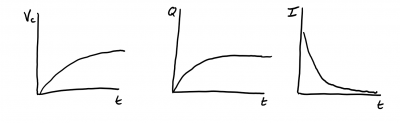
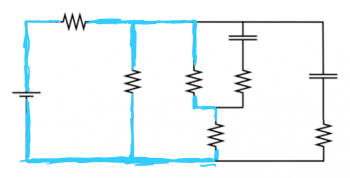
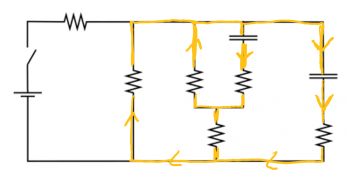
a) Initially there is current in all branches of the circuit (uncharged capacitors act like wires - current can pass through).

b) $I_i = 0.00436 A$

c)

d) Current goes through all branches without a capacitor (charge capacitors act like a break in the circuit - no current)

e) $I_f = 0.0036 A$

f) If the switch is opened, the capacitors would discharge through the resistors below.