Motivating Ampere's Law

Earlier you learned about the Biot-Savart law, which is a way of determining the magnetic field due to moving charges. The Biot-Savart law relies on the principle of superposition, each little charge creates a small contribution to the net magnetic field and we add up all the contributions, often by integrating along the wire, to find the net magnetic field. Here, you will read about another way to determine the magnetic field that exploits the symmetry (or shape) of the situation. This approach called Ampere's law can be conceptually more difficult than Biot-Savart, but is often, mathematically more straight-forward.

The Biot-Savart law, is always true, but it is not always useful for solving problems with pencil-and-paper. Solving problems with Biot-Savart using pencil-and-paper techniques requires that the integral that you construct have a known anti-derivative. That is, the integral that you construct can be integrated into a known function. Now, this might seem to suggest that Biot-Savart is only useful when that's that case, but Biot-Savart can also be used in a computer program. The computer is very good at adding many little bits of something and is able to do so with or without a known anti-derivative. The Biot-Savart Law (either analytically or computationally) can be used in almost any case because it's just a procedure that exploits superposition (adding up of small contributions).

Where Biot-Savart becomes a bit unwieldy is when we want to find the magnetic field due to distributions of currents (termed volume currents) where the symmetry is really simple (e.g., a long thick wire with current throughout). In this case, we will find that Ampere's Law is a nice shortcut to solving these problems. So think of Ampere's Law as a useful analytical technique that can be used in some cases where the symmetry of the situation (as we will see) suggests it's a better choice than Biot-Savart. Ultimately both give you the magnetic field at a location, but sometimes one approach makes the math a bit easier (like Gauss' Law for electric fields).

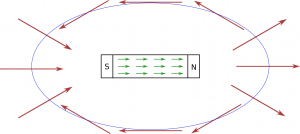
Given the analogy to Gauss' Law, you might think the approach is going to be similar - we integrate the magnetic field over an imagined closed surface area and that tells us something. Unfortunately, as far as a we know (and people are looking!), there are no single magnetic 'charges', termed 'magnetic monopoles.' That is, everywhere we look magnetic poles come in pairs - a north pole and a south pole. For example, if we think about enclosing a bar magnet with a Gaussian-like surface (an imaginary bubble), the magnetic flux through the whole bubble would be zero! For every magnetic field vector pointing into the bubble, there is also a magnetic field vector pointing out.

It turns out that this is true no matter what the source of your magnetic field is (bar magnet, moving charge, or current-carrying wire) - the integral of the magnetic field over a closed surface is always zero. That is, a closed volume never has net magnetic flux assuming that the magnetic field is constant. Mathematically, we would write this as:

$$\int\int\vec{B}\cdot d\vec{A} = 0$$

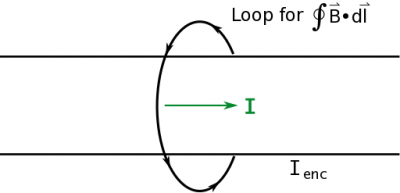
So then, what is Ampere's Law? We want it to relate the field ($\vec{B}$) to the source of the field (i.e., moving charges, $I$). Because these two are related through a vector operation called a curl, the mathematical relationship between them is an integral over an imagined closed loop rather than an imagined closed surface (like with Gauss's Law). Mathematically, we will represent this relationship as:

$$\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}$$

where the imagined loop that we pick has some enclosed current that passes through the surface of the loop (like the example to the right). The next few pages of notes will unpack the parts of this equation and how we can use it to find the magnetic field from a current.