Chapter 21 in Matter and Interactions (4th edition)
Symmetry and Mathematical Tools
One of the important aspects of electromagnetism is understanding the patterns of the electric and magnetic fields that the charges and current produce. These patterns can often suggest a symmetry – a regular order to the pattern that helps us deal with the field. Symmetries are a deep part of physics. In this case, we are discussing geometric symmetries, which suggest that there's a particular kind of charge or current producing the field. These symmetries can be used to reformulate the calculations to find the electric field (Gauss' Law) or magnetic field (Ampere's Law) more simply.
Gauss' Law
Gauss' Law helps us to calculate the electric field when there is sufficient symmetry to use it. That is, Gauss' Law, as mathematical statement, is always true, but it's only useful in limited cases (namely, for planes, cylinders and spheres of charge). The total electric flux is always proportional to the enclosed charge, but that doesn't mean we can always calculate the electric field from Gauss' Law.
$$\Phi_E = \oint \vec{E} \bullet d\vec{A} = \dfrac{q_{enc}}{\varepsilon_0}$$
For a chosen Gaussian surface, if the electric field points the same direction as the area vector everywhere on the surface and we can argue that the electric field is constant in magnitude over the surface, then we can simplify Gauss' Law sufficiently where it becomes useful,
$$\oint \vec{E} \bullet d\vec{A} = E \oint dA = \dfrac{q_{enc}}{\varepsilon_0}$$
The example we have seen a number of times is the point charge, $q$. If we encapsulate the point charge with an imaginary spherical surface of radius $r$, such that the point charge is at the center, we can easily find the electric field of the charge,
$$\oint \vec{E} \cdot d\vec{A} = \dfrac{q_{enc}}{\varepsilon_0}$$ $$E \oint dA = \dfrac{q}{\varepsilon_0}$$ $$E 4\pi r^2 = \dfrac{q}{\varepsilon_0}$$ $$E = \dfrac{q}{4\pi\varepsilon_0 r^2}$$
where we understand the direction to point radially outward as usual for a positive point charge. This was necessary to argue the simplification of Gauss' Law from the first to the second line.
Ampere's Law
Ampere's Law helps us calculate the magnetic field when there is sufficient symmetry to use it. Like Gauss' Law, Ampere's Law, as a mathematical statement, is always true, but it's only useful in limited contexts (like long wires or solenoids). The total integral around any closed loop is always proportional to the total current enclosed by the loop, but that doesn't mean we can compute the magnetic field using Ampere's Law for every case,
$$\oint \vec{B} \bullet d\vec{l} = \mu_0 I_{enc}.$$
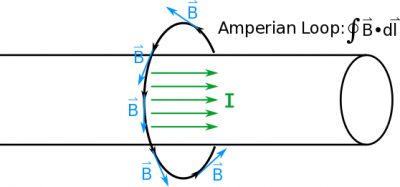
For a chosen Amperian loop, if the magnetic field aligns with the direction of the loop and we can argue that the magnetic field is constant over the loop (or part of it and zero elsewhere), then we can simplify Gauss' Law sufficiently where it becomes useful,
$$\oint \vec{B} \bullet d\vec{l} = B \oint dl = \mu_0 I_{enc}.$$
The example that we have seen a number of times is the very long thin wire with current $I$. If we encircle the wire with a loop of radius $r$ with the wire centered inside the loop, we can easily find the magnetic field,
$$\oint \vec{B} \bullet d\vec{l} = \mu_0 I_{enc}$$ $$B \oint dl \mu_0 I$$ $$B 2 \pi r = \mu_0 I$$ $$B = \dfrac{\mu_0 I}{2 \pi r}.$$
where we understand the magnetic field to loop around the wire as given by the right hand rule. This was necessary to argue for the simplification of Ampere's Law from the first to the second line.