Project: Restarting I.A.N.
Kick Off Questions
- What is the equation for combining capacitors in series? What about in parallel? How is this similar/different to resistors?
- The equation for energy stored in a capacitor can be written in 3 different ways - what are the 3 ways & how do you get them?
- What are the loop and node rule? How do they apply for capacitors?
Main Problem
Your makeshift defibrillator was successful and I.A.N. powered back up. But before you send him into the accelerator hall to place the radiation shielding, Director Lewis wants to make sure his programming is still working properly – a malfunctioning robot in the accelerator hall could lead to disaster. She's prepared a list of questions to validate his logic circuitry, and has asked you to work out the solutions and check his answers while she collects the shielding for I.A.N. to place around the accelerator.
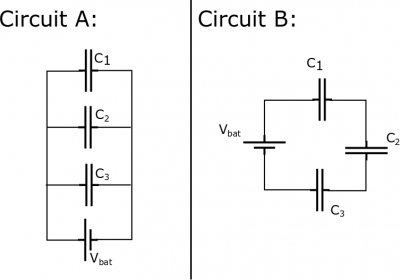
Level 1: Basic Combos
For the circuits below, say that $V_{bat} = 5 \;{\rm V}$, $C_1 = 6 \; \mu{\rm F}$, $C_2 = 7 \;\mu{\rm F}$, and $C_3 = 8\; \mu{\rm F}$. For each circuit below,
a) What is the equivalent capacitance of the circuit?
b) Which capacitor would have the largest voltage drop?
c) Which capacitor would have the smallest charge?
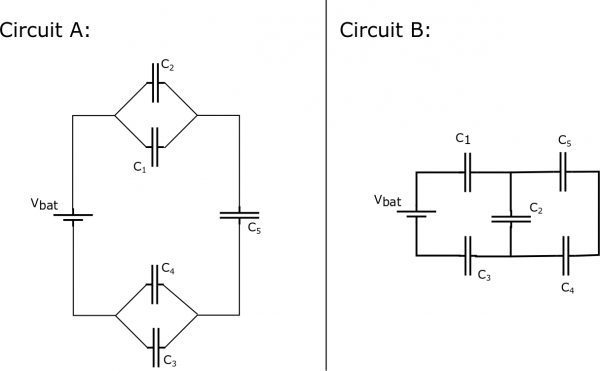
Level 2: Equal circuit elements
For the circuits below, say that $V_{bat} = 16 \; {\rm V}$ and each capacitor is $C = 470 \; \mu{\rm F}$. For each circuit,
a) Which capacitors are in series? Which capacitors are in parallel? How do you know?
b) What is the equivalent capacitance of the circuit?
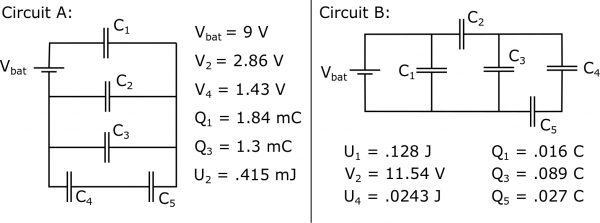
Level 3: Capacitor Circuits
For the circuits below, you have been given some of the quantities for various elements around the circuit. For example, $V_1$ would correspond to the voltage across Capacitor 1. For each circuit,
a) Which capacitors are in series and which capacitors are in parallel? How do you know?
b) Find all the missing quantities for each capacitor (C, V, Q, and U).
c) What is the voltage provided by the battery in your circuit?
d) What is the total charge stored by the circuit? What is the total energy?
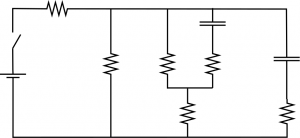
Level 4: Challenge Mode
Consider the circuit below where initially the capacitors are all uncharged.
a) Initially (the moment that the switch is closed), where is there current in the circuit?
b) When the switch is closed, what is the initial current provided by the battery if $V_{bat} = 6V$, all resistors are $R = 1000 \Omega$, and all capacitors are $C = 2200 mF$?
c) What would the V vs t, Q vs t, and I vs t graphs look like for each of the capacitors?
d) After the switch has been closed for a long time, where is there current in the circuit?
e) What is the final current provided by the battery? (After the switch has been closed for a long time.)
f) When the switch has been closed for a long time, what is the voltage across each of the capacitors?
g) If the switch is then opened again, what would you expect to happen? Explain in words.
Learning Goals:
- Explain how you know something is in series. Explain what happens for charge & voltage when capacitors are in series.
- Explain how you know something is in parallel. Explain what happens for charge & voltage when capacitors are in parallel.
- Explain what the loop rule is and the physical principle it is related to.
- Explain what the node rule is and the physical principle it is related to.
- Apply $C = Q/V$ & $ U = 1/2C V^2$ to solve for any unknown quantities in the circuit (U, Q, V, & C).
- Calculate the total combined capacitance for a given circuit.
Wrap Up Questions
- What are the circuit rules that you used to solve these circuits? When did you use each of them?
- How do the circuit rules for capacitors compare to circuit rules for resistors? Divide a whiteboard in 2 and write them out!
- How do you know if capacitors are in series or parallel (or neither)? What happens to current & voltage in each of those cases?
- What assumptions did you make when solving these circuits? (Hint: there are at least 3 big ones.)
- Why do we use energy when talking about capacitors? Why do we use power when talking about resistors?