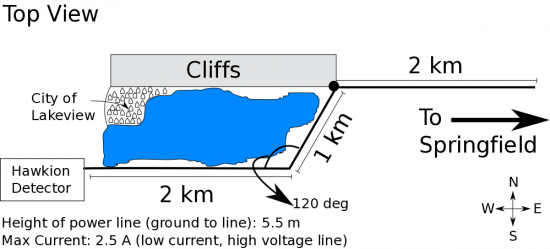
You've just received a phone call from the head of the Wildlife Tracking Foundation of Lakeview. Dr. O'Taulest who started an investigation into the cliff region of Lakeview due to the finding of previosuly unfound multicolored excrement. The report from this investigation did not explain the origin of the poop but did report that they have recently had an unprecedented disappearance of their green-bellied canaries that like to roost in the cliffs overlooking the lake. Their most popular nesting area on the eastern edge of the cliffs is completely empty. It's almost like they decided to migrate 4 months ahead of schedule! The Wildlife Tracking Foundation is also reporting that the fish, especially those near the north-eastern bank of the lake, have suffered a sudden decrease in their population. Dr. O'Taulest claims that it is all your fault since you had to build a large power line to run the Hawkion detector. Clearly, the magnetic field from the power line interfered with the green-bellied canaries (who rely on Earth's magnetic field for migration purposes), causing their vacation from the vicinity.

As consultants on the Hawkion project, you have been asked to kindly disprove Dr. O'Taulest's claims. The government does not need any more press about Lakeview getting out given the continued storm front inhabiting the town. To start, you go back and consult the handy-dandy blueprints you drew up when designing the transmission line.

Task force S.P.A.R.T.A.N has been given some much-needed downtime. Your team goes for a walk around town in order to get to know some members of the community and find the best coffee in town. As you are strolling around town, you hear a holler. “Aya!!! Hey, howdy!! Come check out this ol' piece of junk I got right here, y'all!” It's Dr. Daryn McPaddel, the town inventor/engineer who is always showing her neighbors' strange contraptions that she has made, and also happens to live adjacent to Lakeview's scrapyard, which allows her to tinker and invent to her heart's delight. This is what you see:

As you observe Dr. McPaddel's magnetic crane-thing at work you notice that there are a bunch of kids on a field trip in the scrap yard. This seems like an odd place for a field trip but then again nobody can really leave the town so there might not be a load of options. The teacher with the field trip, identifying you from all your work around town approaches you and says: “Hey, you know about electricity and magnets and whatnot, can you explain what's going on?” You agree to explain in detail how the thing works since you are concerned what crazy old Dr. Daryn McPaddel will say. The best way would probably be with a visual, and Dr. McPaddel has already created a visual of the coil of wire inside the contraption. All that's left to do is show what the magnetic field looks like.

GlowScript 2.7 VPython
xaxis = cylinder(pos = vec(-3, 0, 0), axis = vec(6, 0, 0), radius = 0.01, color = color.white)
yaxis = cylinder(pos = vec(0, -3, 0), axis = vec(0, 6, 0), radius = 0.01, color = color.white)
zaxis = cylinder(pos = vec(0, 0, -3), axis = vec(0, 0, 6), radius = 0.01, color = color.white)
 
## Setting up the constants
mu0 = 4 * pi * 10 ** -7    # magnetic constant in standard units
I = 5000                   # current in ring
R = 1                      # radius of ring
thickness = 0.05           # thickness of ring
 
## Drawing the ring
ring = ring(pos = vec(0, 0, 0), axis = vec(0, 0, 1), size = vec(thickness, 2 * R, 2 * R), color = color.blue)
 
## Splitting the ring into little pieces
N = 100                    # number of little pieces
dtheta = 2 * pi / N        # angle between adjacent little pieces
theta = 0
little_pieces = []
 
## Determining dl and the location for each little piece
while theta < 2 * pi:
    r_source = vec(0, 0, 0)
    dl = vec(0, 0, 0)
 
    little_piece = arrow(pos = r_source, axis = dl, color = color.green)
    little_pieces.append(little_piece)
 
    theta = theta + dtheta
 
## Picking some points to observe the magnetic field
observation_radii = [0, 0.4, 0.8, 1.2, 1.6]
observation_angles = [0, pi/2, pi, 3*pi/2]
observation_heights = [0]
r_obs_vectors = []
 
## Putting the observation points into a list
for rad in observation_radii:
    for angle in observation_angles:
        for height in observation_heights:
            r_obs = vec(rad * cos(angle), rad * sin(angle), height)
            r_obs_vectors.append(r_obs)
 
## Visualizing the magnetic field
for r_obs in r_obs_vectors:
    B_total = vec(0, 0, 0)
    for little_piece in little_pieces:
        r_source = little_piece.pos
        dl = little_piece.axis
 
        r_sep = vec(0, 0, 0)
        B_little_piece = vec(0, 0, 0)
 
        B_total = B_total + B_little_piece
    arrow(pos = r_obs, axis = B_total, color = color.yellow)