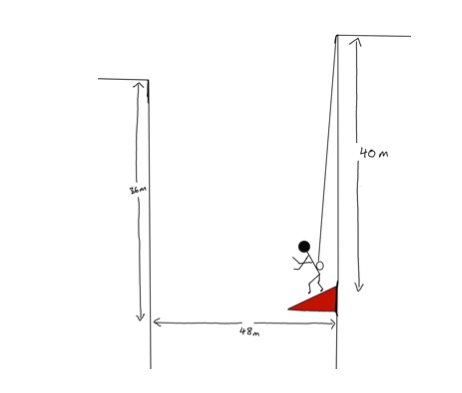
Ethan Hunt (our stunt person) is rap jumping down a building to try and get to an adjacent building. He attaches one end of a grapple to the top of the building and the other end leads to a spindle wheel (m = 0.5 kg) of wire that unwinds as he moves away from the grapple. The wheel is specifically designed so that once it begins to spin it is very difficult to make it stop. His goal is the rap jump down one building to a canopy that is positioned diagonally so that he can spring from that canopy across to the other building. See diagram below. The spindle wheel has an outer radius of 6.2cm and an inner radius of 2cm. Ethan drops down to the canopy 40 meters down. The building he is trying to get to is 48 meters horizontally from the original building and 36 meters vertically high. The spring constant of the canopy has been tested to be 120 N/m and the stunt person is trained to bounce off the canopy at a 45 degree angle to the horizontal. At what speed does Ethan make it to the other building with? (Figure below.)

Once our stunt person who is playing Ethan is on top of the building an attack drone flies down to attack him. It turns out he had another spindle wheel of exactly the same dimensions and mass attached to him as the first wheel (m = 0.5 kg, the outer radius of 6.2cm and an inner radius of 2cm) and the drone has latched onto this and started pulling with a force equivalent to the force of gravity that was applied to Ethan as he fell from the building. This force is being applied directly horizontally to Ethan so that the drone is trying to pull him off the top of the building. Meanwhile, Ethan is still attached to the wire that helped him get to the top of this new building. Ethan is 25 meters from the edge of the building. How far does the drone have to travel so that Ethan will be at the edge of the building and what speed will Ethan be traveling at when he gets there?

Some initial testing of spindle wheels of different masses and radii have shown (for a constant force) that the relationship between the angular speed of the reel and the linear speed of Ethan is related to the ratio of the masses of the Ethan and reel. The equation that best fits this data is given below,

$$\omega_{\rm wheel} = \dfrac{M_{\rm ethan}}{m_{\rm wheel}}\dfrac{v_{\rm ethan}}{R_{\rm wheel}}$$