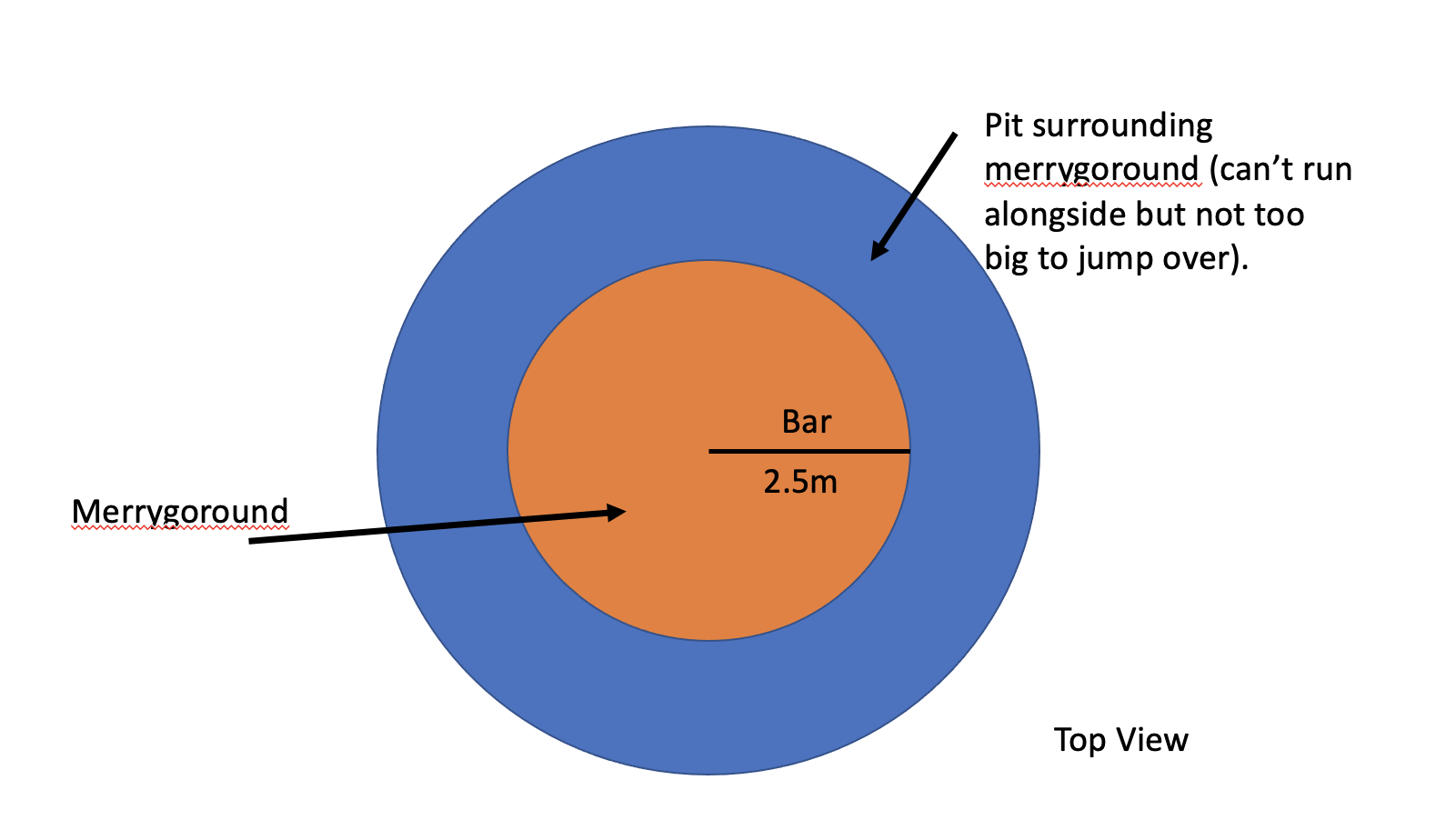
For some reason, the area in which you live in keeps on going through periods of blackouts where you have no power. You decide that you need to build an alternative generator using a merry-go-round. The merry-go-round ride has one bar moving from the centre of the ride to a point at the edge of the ride. In building your generator you have to dig up the perimeter of merrygoround in order to accomodate all the piping needed to develop it and this has resulted in you being unable to run alongside the merrygoround pushing it. Which means you are going to have to create a collision with the bar somehow in order to make the merry-go-round rotate to create energy. You need to figure out what velocity the mass you have chosen to collide with the bar needs to be in order to achieve your goal generating 6500 Joules in order to create enough electricity to keep your phone charged. You also have available to you seven 5kg weights with some straps. The uniform density disk that comprises the ride is 300kg and has a radius of 2.5m. Your team which is working on the roundabout consists of 4 members.

The idea here is to have the group of people run and land on the platform.

For review, angular momentum outlines and formulas can be found in the Angular Momentum Notes

The initial momentum of the group of people having total mass $\tilde{m}$ running with a velocity $v$ is given by $p=\tilde{m}v$, where $\tilde{m}=q\mathcal{M}+sm$ is the total mass of the group ($q$ is the number of people in the group and $s$ is the number of bags that are being carried along). Accordingly, the initial angular momentum as measured from the axis of the platform is given by $$L_{i}=r\tilde{m}v,$$ where $r$ is the distance from the axle of the platform.

After landing on the platform (we assume they all land at the maximum possible radius $r$), we know that it will rotate with angular velocity $\omega$. Since angular momentum is conserved, we must have \begin{eqnarray*}L_{i}&=&L_{f}\\ r\tilde{m}v&=&I\omega.\end{eqnarray*}

Now, to get rid of $\omega$, we must recognize the relationship between energy (formula for rotation kinetic energy can be review in Rotational Kinetic Energy notes) and angular velocity: $$\frac{1}{2}I\omega^{2}=E_{\rm min}\qquad\longrightarrow\qquad \omega=\sqrt{\frac{2E_{\rm min}}{I}}.$$

Combining everything together, we have \begin{eqnarray*}r\tilde{m}v&=&I\omega\\r\tilde{m}v&=&I\sqrt{2E_{\rm min}/I}\\r\tilde{m}v&=&\sqrt{2E_{\rm min}I}\end{eqnarray*} Finally, this can be solved for either the mass $\tilde{m}$ that must be used, or the velocity $v$ that must be acquired by the group.