In the notes, you will read about the formal derivation to separate the total kinetic energy into a translational component that tracks the energy associated with the motion of the center of mass, and the relative component that that tracks the energy of due to the motion relative to the center of mass.

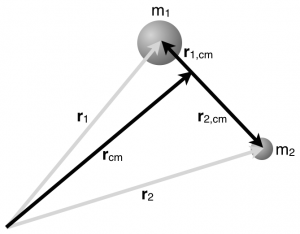
Begin by considering two particles, one of mass $m_1$ at location $\vec{r}_1$ measured relative to some fixed coordinate axes and the other of mass $m_2$ at location $\vec{r}_2$ measured relative to the same coordinate axes. Both of these vectors positions are indicated with grey arrows.

For these two particles, we could determine their center of mass,

$$\vec{r}_{cm} = \dfrac{m_1\,\vec{r}_1 + m_2\,\vec{r}_2}{m_1+m_2}$$

which is indicated by a black arrow, and then measure their positions relative to the center of mass ($\vec{r}_{1,cm}$ and $\vec{r}_{2,cm}$, also black arrows in the figure). The location of each particle can be related to these vectors,

$$\vec{r}_1 = \vec{r}_{cm} + \vec{r}_{1,cm} \qquad \vec{r}_2 = \vec{r}_{cm} + \vec{r}_{2,cm}$$

So in general you could have a collection of many particles each with a location vector given by,

$$\vec{r}_i = \vec{r}_{cm} + \vec{r}_{i,cm}$$